练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．已知x2-3x-1=0，求：
    （1）x2+$\frac{1}{{x}^{2}}$的值；
    （2）（x-2）（$\frac{1}{x}$+2）的值．

    分析 根据x2-3x-1=0，两边同时除以x得到：x-3-$\frac{1}{x}$=0，从而得到x-$\frac{1}{x}$=3，然后变形求解即可．

    解答 解：∵x2-3x-1=0，
    ∴两边同时除以x得到：x-3-$\frac{1}{x}$=0，
    ∴x-$\frac{1}{x}$=3，
    （1）x2+$\frac{1}{{x}^{2}}$=（x-$\frac{1}{x}$）2+2=9+2=11；
    （2）（x-2）（$\frac{1}{x}$+2）=2（x-$\frac{1}{x}$）-3=2×3-3=3．

    点评 本题考查了一元二次方程的解的知识及分式的混合运算，属于基础题，难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．某服装厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：①买一套西装送一条领带；②西装和领带都按定价的90%付款．
    现某客户要到该服装厂购买西装20套，领带x条（x＞20）：
    （1）若该客户按方案①购买，需付款（40x+3200）元（用含x的代数式表示）；（答案写在下面）
    若该客户按方案②购买，需付款（36x+3600）元 （用含x的代数式表示）；（答案写在下面）
    （2）若x=30，通过计算说明此时按哪种方案购买较为合算？
    （3）当x=30时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

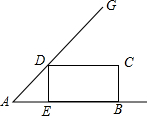    8．如图，∠A=45°，AB=30，点E在线段AB上运动，过点E作DE⊥AB，交AG于点D．以DE、EB为邻边作矩形BCDE．将△ADE沿直线DE翻折，使点A落在点F处．设矩形BCDE与△ADF重叠部分的面积为S，线段DE的长为x（0＜x＜30）．
    （1）线段EF的长为x．（用含x的代数式表示）
    （2）当矩形BCDE为正方形，求x的值．
    （3）求S与x之间的函数关系式．
    （4）若线段DF把矩形BCDE分成面积比为1：3的两部分，直接写出此时x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．已知第一个三角形的面积是1，它的三条中位线组成第1个三角形，第2个三角形的三条中位线又组成第3个三角形，以此类推…第2014个三角形的面积为（　　）
    A．$\frac{1}{{2}^{4022}}$B．$\frac{1}{{2}^{4024}}$C．$\frac{1}{{2}^{4026}}$D．$\frac{1}{{2}^{4028}}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．用反证法，求证：两条直线被第三条直线所截，如果内错角不相等，那么这两条直线不平行．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．去年10月，国民体质监测中心等机构开展了青少年形体测评，专家组随机抽查了某市500名初中学生坐姿、站姿、走姿的好坏情况，数据如表：
     坐姿不良站姿不良 走姿不良 三姿良好 
     100155 185 60 
    我们要想知道每种形体占所抽查总人数的百分比，需对专家的测评数据作适当处理，画出适当的统计图，应选择什么统计图呢？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，在平面直角坐标系中，点A的坐标为（0，$\frac{29}{2}$），直线y=-$\frac{5}{12}$x-5与x轴、y轴分别交于B、C，点P是直线BC上的一个动点，则AP长的最小值为18．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在平面直角坐标系中，点A和点B分别在x轴的正半轴和y轴的正半轴上，且OA=6，OB=8，点D是AB的中点．
    （1）直接写出点D的坐标及AB的长；
    （2）若直角∠NDM绕点D旋转，射线DP分别交x轴、y轴于点P、N，射线DM交x轴于点M，连接MN．
    ①当点P和点N分别在x轴的负半轴和y轴的正半轴时，若△PDM∽△MON，求点N的坐标；
    ②在直角∠NDM绕点D旋转的过程中，∠DMN的大小是否会发生变化？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．甲、乙两地相距a千米，小李计划3小时由甲地到乙地，如果想提前1小时到达，那么每小时应多走$\frac{a}{6}$千米．

    查看答案和解析>>

    同步练习册答案