
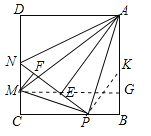
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ4ЕФе§ЗНаЮABCDжаЃЌPЪЧBCБпЩЯвЛЖЏЕуЃЈВЛКЌBЁЂCСНЕуЃЉЃЌНЋЁїABPбижБЯпAPЗелЃЌЕуBТфдкЕуEДІЃЛдкCDЩЯгавЛЕуMЃЌЪЙЕУНЋЁїCMPбижБЯпMPЗелКѓЃЌЕуCТфдкжБЯпPEЩЯЕФЕуFДІЃЌжБЯпPEНЛCDгкЕуNЃЌСЌНгMAЃЌNAЃЎдђвдЯТНсТлжае§ШЗЕФга ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
ЂйЁїCMPЁзЁїBPAЃЛ
ЂкЫФБпаЮAMCBЕФУцЛ§зюДѓжЕЮЊ10ЃЛ
ЂлЕБPЮЊBCжаЕуЪБЃЌAEЮЊЯпЖЮNPЕФжаДЙЯпЃЛ
ЂмЯпЖЮAMЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЂнЕБЁїABPЁеЁїADNЪБЃЌBP=![]() ЃЎ
ЃЎ

ЁОД№АИЁПЂйЂкЂнЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЁпЁЯAPB=ЁЯAPEЃЌЁЯMPC=ЁЯMPNЃЌЁпЁЯCPN+ЁЯNPB=180ЁуЃЌЁр2ЁЯNPM+2ЁЯAPE=180ЁуЃЌЁрЁЯMPN+ЁЯAPE=90ЁуЃЌЁрЁЯAPM=90ЁуЃЌЁпЁЯCPM+ЁЯAPB=90ЁуЃЌЁЯAPB+ЁЯPAB=90ЁуЃЌЁрЁЯCPM=ЁЯPABЃЌЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌЁрAB=CB=DC=AD=4ЃЌЁЯC=ЁЯB=90ЁуЃЌЁрЁїCMPЁзЁїBPAЃЎЙЪЂйе§ШЗЃЌЩшPB=xЃЌдђCP=4ЉxЃЌЁпЁїCMPЁзЁїBPAЃЌЁр![]() ЃЌЁрCM=
ЃЌЁрCM=![]() xЃЈ4ЉxЃЉЃЌЁрSЫФБпаЮAMCB=
xЃЈ4ЉxЃЉЃЌЁрSЫФБпаЮAMCB=![]() [4+
[4+![]() xЃЈ4ЉxЃЉ]ЁС4=
xЃЈ4ЉxЃЉ]ЁС4=![]() =
=![]() ЃЌЁрx=2ЪБЃЌЫФБпаЮAMCBУцЛ§зюДѓжЕЮЊ10ЃЌЙЪЂке§ШЗЃЌЕБPB=PC=PE=2ЪБЃЌЩшND=NE=yЃЌдкRTЁїPCNжаЃЌ
ЃЌЁрx=2ЪБЃЌЫФБпаЮAMCBУцЛ§зюДѓжЕЮЊ10ЃЌЙЪЂке§ШЗЃЌЕБPB=PC=PE=2ЪБЃЌЩшND=NE=yЃЌдкRTЁїPCNжаЃЌ![]() НтЕУ
НтЕУ![]() ЃЌЁрNEЁйEPЃЌЙЪЂлДэЮѓЃЌзїMGЁЭABгкGЃЌЁпAM=
ЃЌЁрNEЁйEPЃЌЙЪЂлДэЮѓЃЌзїMGЁЭABгкGЃЌЁпAM=![]() =
=![]() ЃЌЁрAGзюаЁЪБAMзюаЁЃЌЁпAG=ABЉBG=ABЉCM=4Љ
ЃЌЁрAGзюаЁЪБAMзюаЁЃЌЁпAG=ABЉBG=ABЉCM=4Љ![]() xЃЈ4ЉxЃЉ=
xЃЈ4ЉxЃЉ=![]() ЃЌЁрx=1ЪБЃЌAGзюаЁжЕ=3ЃЌЁрAMЕФзюаЁжЕ=
ЃЌЁрx=1ЪБЃЌAGзюаЁжЕ=3ЃЌЁрAMЕФзюаЁжЕ=![]() =5ЃЌЙЪЂмДэЮѓЃЎ
=5ЃЌЙЪЂмДэЮѓЃЎ
ЁпЁїABPЁеЁїADNЪБЃЌЁрЁЯPAB=ЁЯDAN=22.5ЁуЃЌдкABЩЯШЁвЛЕуKЪЙЕУAK=PKЃЌЩшPB=zЃЌЁрЁЯKPA=ЁЯKAP=22.5ЁуЃЎЁпЁЯPKB=ЁЯKPA+ЁЯKAP=45ЁуЃЌЁрЁЯBPK=ЁЯBKP=45ЁуЃЌЁрPB=BK=zЃЌAK=PK=![]() zЃЌЁрz+
zЃЌЁрz+![]() z=4ЃЌЁрz=
z=4ЃЌЁрz=![]() ЃЌЁрPB=
ЃЌЁрPB=![]() ЙЪЂне§ШЗЃЎ
ЙЪЂне§ШЗЃЎ
ЙЪД№АИЮЊЃКЂйЂкЂнЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.a2+a3=a5
B.ЃЈa2ЃЉ3=a5
C.2a3a=6a
D.ЃЈ2a3bЃЉ2=4a6b2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯAЃН52ЁуЃЌЁЯABCгыЁЯACBЕФНЧЦНЗжЯпНЛгкD1ЃЌЁЯABD1гыЁЯACD1ЕФНЧЦНЗжЯпНЛгкЕуD2ЃЌвРДЫРрЭЦЃЌЁЯABD4гыЁЯACD4ЕФНЧЦНЗжЯпНЛгкЕуD5ЃЌдђЁЯBD5CЕФЖШЪ§ЪЧ ( )

A. 56Ёу B. 60Ёу C. 68Ёу D. 94Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуMЃЈЉ3ЃЌЉ5ЃЉЪЧгЩNЯШЯђЩЯЦНвЦ4ИіЕЅЮЛЃЌдйЯђзѓЦНвЦ3ИіЕЅЮЛЖјЕУЕНЃЌдђЕуNЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A.ЃЈ0ЃЌЉ9ЃЉ
B.ЃЈЉ6ЃЌЉ1ЃЉ
C.ЃЈ1ЃЌЉ2ЃЉ
D.ЃЈ1ЃЌЉ8ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕШбќжБНЧЁїABCжаЃЌЁЯACB=90ЁуЃЌCOЁЭABгкЕуOЃЌЕуDЁЂEЗжБ№дкБпACЁЂBCЩЯЃЌЧвAD=CEЃЌСЌНсDEНЛCOгкЕуPЃЌИјГівдЯТНсТлЃК
ЂйЁїDOEЪЧЕШбќжБНЧШ§НЧаЮЃЛЂкЁЯCDE=ЁЯCOEЃЛЂлШєAC=1ЃЌдђЫФБпаЮCEODЕФУцЛ§ЮЊ![]() ЃЛЂм
ЃЛЂм![]() ЃЌЦфжаЫљгае§ШЗНсТлЕФађКХЪЧ ЃЎ
ЃЌЦфжаЫљгае§ШЗНсТлЕФађКХЪЧ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбЖрЯюЪН 3ЃЈxЉyЃЉ2+2ЃЈyЉxЃЉ3 ЗжНтвђЪННсЙће§ШЗЕФЪЧЃЈ ЃЉ
A.ЃЈxЉyЃЉ2ЃЈ3Љ2xЉ2yЃЉB.ЃЈxЉyЃЉ2ЃЈ3Љ2x+2yЃЉ
C.ЃЈxЉyЃЉ2ЃЈ3+2xЉ2yЃЉD.ЃЈyЉxЃЉ2ЃЈ3+2xЉ2yЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИажЊЃКШчЭМ1ЃЌADЦНЗжЁЯBACЃЎЁЯB+ЁЯC=180ЁуЃЌЁЯB=90ЁуЃЌвзжЊЃКDB=DCЃЎ
ЬНОПЃКШчЭМ2ЃЌADЦНЗжЁЯBACЃЌЁЯABD+ЁЯACD=180ЁуЃЌЁЯABDЃМ90ЁуЃЌЧѓжЄЃКDB=DCЃЎ
гІгУЃКШчЭМ3ЃЌЫФБпаЮABCDжаЃЌЁЯB=45ЁуЃЌЁЯC=135ЁуЃЌDB=DC=aЃЌдђABЉAC= ЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЖўДЮКЏЪ§yЃНЉx2+2x+1ЕФЭМЯѓжаЃЌШєyЫцxЕФдіДѓЖјМѕЩйЃЌдђxЕФШЁжЕЗЖЮЇЪЧЃЈЁЁЁЁЃЉ
A.xЃМ1B.xЃО1C.xЃМЉ1D.xЃОЉ1
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com