练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在二次函数y＝﹣x2+2x+1的图象中，若y随x的增大而减少，则x的取值范围是（　　）

    A.x＜1B.x＞1C.x＜﹣1D.x＞﹣1

    【答案】B

    【解析】

    先配方得到抛物线的对称轴为直线x＝1，然后根据二次函数的性质求解．

    解：y＝﹣x2+2x+1＝﹣（x﹣1）2+2，

    抛物线的对称轴为直线x＝1，

    ∵a＝﹣1＜0，

    ∴当x＞1时，y随x的增大而减少．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为4的正方形ABCD中，P是BC边上一动点（不含B、C两点），将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有 （写出所有正确结论的序号）

    ①△CMP∽△BPA；

    ②四边形AMCB的面积最大值为10；

    ③当P为BC中点时，AE为线段NP的中垂线；

    ④线段AM的最小值为；

    ⑤当△ABP≌△ADN时，BP=．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=2x2向右平移1个单位，再向上平移5个单位，则平移后的抛物线的解析式为( )
    A.y=2(x+1)2+5
    B.y=2(x+1)2-5
    C.y=2(x-1)2-5
    D.y=2(x-1)2+5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．

    求证：．

    该同学仔细分析后，得到如下解题思路：

    先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证．

    （1）请你根据以上解题思路帮尤秀同学写出证明过程．

    （2）利用题中的结论，解答下列问题：

    在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E，F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】多项式4x2+1加上一个单项式后,使它成为一个整式的完全平方,那么加上的单项式可以从①-1;②4x;③-4x;④4x4中选取( )
    A.①②
    B.②③
    C.③④
    D.①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，大海中某灯塔P周围10海里范围内有暗礁，一艘海轮在点A处观察灯塔P在北偏东60°方向，该海轮向正东方向航行8海里到达点B处，这时观察灯塔P恰好在北偏东45°方向．如果海轮继续向正东方向航行，会有触礁的危险吗？试说明理由．（参考数据：≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

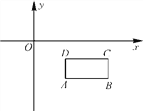
    【题目】如图，已知长方形ABCD四个顶点的坐标分别是A(2，－2)，B(5，－2)，C(5，－)，D(2，－).

    (1)四边形ABCD的面积是多少；

    (2)将四边形ABCD向上平移个单位长度，求所得的四边形A′B′C′D′的四个顶点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知EC∥AB，∠EDA=∠ABF．

    （1）求证：四边形ABCD是平行四边形；

    （2）求证：=OEOF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种细菌在培养过程中，每半小时分裂一次（由一个分裂成两个），若这种细菌由1个分裂为64个，则这个过程要经过（　　）

    A. 1小时 B. 2小时 C. 3小时 D. 4小时

    查看答案和解析>>

    同步练习册答案