�⣺��1����������OABC�������9��
��AB=BC=3��
��B��������3��3����
��B��3��3�����뺯��y=

�У�
��k=xy=9��
��2����P��a��
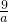
������a��3������PG=a-3��PE=
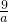
��
��S
�ı���AEPG=PG��PE=

���ã�a-3��•
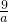
=

��
���a=6����P��6��

����
��ֱ��PA����ʽΪy=kx+b����P��6��

����A��3��0������������룬
��

��
���
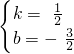
��
��ֱ��PA�Ľ���ʽΪy=

x-

��
��3���ߵ�P��m��n����˫����y=

�ϣ�
��n=
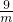
��
��y=m+n=m+
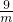
��2

=6��
�ຯ��y=m+n����СֵΪ6��
��������1������������OABC�������9������B������Ϊ��3��3������B��������뺯��y=

������k=9��
��2����P��a��
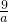
������a��3������PG=a-3��PE=
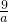
����S
�ı���AEPG=PG��PE=

���з�����a����ֱ��PA����ʽΪy=kx+b����P��A��������������ֱ��PA�Ľ���ʽ��
��3����P��m��n����˫����y=

�ϣ���֪n=
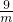
����y=m+n=m+
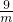
���ٸ���ƽ��ֵ��������Сֵ��
������������Ҫ���鷴������������ʽ��һ�κ�������ʽ����ע��ͨ���ⷽ���������꣬�з�������ֱ�ߵĽ���ʽ��ͬʱҪע���������ν�ϵ�˼�룮

 ��ͼ��������OABC�������9����OΪ����ԭ�㣬��A��x���ϣ���C��y���ϣ���B����P��m��n���ں���y=
��ͼ��������OABC�������9����OΪ����ԭ�㣬��A��x���ϣ���C��y���ϣ���B����P��m��n���ں���y= ��k��0��x��0����ͼ���ϣ�����P�ֱ���x�ᡢy��Ĵ��ߣ�����ΪE��F��
��k��0��x��0����ͼ���ϣ�����P�ֱ���x�ᡢy��Ĵ��ߣ�����ΪE��F�� ʱ����PA���ڵ�ֱ�߷��̣�
ʱ����PA���ڵ�ֱ�߷��̣� �����ҽ���a=bʱ�Ⱥų�������
�����ҽ���a=bʱ�Ⱥų������� �У�
��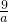 ������a��3������PG=a-3��PE=
������a��3������PG=a-3��PE=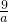 ��
�� ���ã�a-3��•
���ã�a-3��•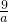 =
= ��
�� ����
���� ����A��3��0������������룬
����A��3��0������������룬 ��
��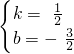 ��
�� x-
x- ��
�� �ϣ�
�ϣ�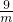 ��
��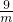 ��2
��2 =6��
=6�� ������k=9��
������k=9��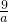 ������a��3������PG=a-3��PE=
������a��3������PG=a-3��PE=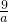 ����S�ı���AEPG=PG��PE=
����S�ı���AEPG=PG��PE= ���з�����a����ֱ��PA����ʽΪy=kx+b����P��A��������������ֱ��PA�Ľ���ʽ��
���з�����a����ֱ��PA����ʽΪy=kx+b����P��A��������������ֱ��PA�Ľ���ʽ�� �ϣ���֪n=
�ϣ���֪n=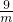 ����y=m+n=m+
����y=m+n=m+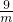 ���ٸ���ƽ��ֵ��������Сֵ��
���ٸ���ƽ��ֵ��������Сֵ��

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
 �Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϲ��ֵ����ΪS������ʾ�����ǵ�P�ڵ�B�������Ҳ����������
�Ĵ��ߣ�����ֱ�ΪE��F���������OEPF��������OABC���غϲ��ֵ����ΪS������ʾ�����ǵ�P�ڵ�B�������Ҳ���������� ��ͼ��������OABC��ADEF�Ķ���A��D��C���������ϣ���F��AB�ϣ���B��E�ں���y=
��ͼ��������OABC��ADEF�Ķ���A��D��C���������ϣ���F��AB�ϣ���B��E�ں���y= ��ͼ��������OABC��������ADEF�Ķ���A��D��C���������ϣ���F��AB�ϣ���B��E�ں���y=
��ͼ��������OABC��������ADEF�Ķ���A��D��C���������ϣ���F��AB�ϣ���B��E�ں���y= ��ͼ��������OABC��������ODEF��λ��ͼ�Σ�OΪλ�����ģ����Ʊ�Ϊ1��
��ͼ��������OABC��������ODEF��λ��ͼ�Σ�OΪλ�����ģ����Ʊ�Ϊ1�� ���ϣ���P��m��n���Ǻ���y=
���ϣ���P��m��n���Ǻ���y=