
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的大小为_________度.
的大小为_________度.
【答案】![]() 或
或![]()
【解析】
分两种情况考虑,∠BAC为锐角时,由AB=BD得∠D=∠DAB,由AB=AC得∠ABC=∠C,根据三角形外角性质可推出∠C=2∠D,根据直角三角形的两锐角互余可得∠C=60![]() ;同理,∠BAC为钝角时,可推出∠ADC=2∠C,根据直角三角形的两锐角互余可得∠C=30
;同理,∠BAC为钝角时,可推出∠ADC=2∠C,根据直角三角形的两锐角互余可得∠C=30![]() .
.
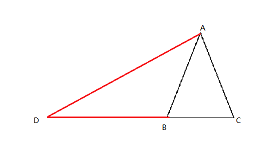
如图所示,若顶角∠BAC为锐角,则:
AB=BD,∠D=∠DAB
∵AB=AC∴∠ABC=∠C,
∴∠C=∠ABC=∠D+∠DAB=2∠D,
∵![]() ,
,
∴∠DAC=90![]() ,
,
∴∠C+∠D=3∠D=90![]() ,
,
∴∠D=30![]() ,
,
∴∠C=2∠D =60![]() ;
;

如图所示,若顶角∠BAC 为钝角,则:
AD=BD,∠B=∠DAB ,
∴∠ADC=∠B+∠DAB=2∠B,
∵AB=AC∴∠B=∠C,
∵![]() ,
,
∴∠DAC=90![]() ,
,
∴∠ADC+∠C=3∠C =90![]() ,
,
∴∠C =30![]() .
.
故答案为:30或60.


科目:初中数学 来源: 题型:
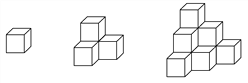
【题目】如图棱长为a的小正方体,按照下图的方法继续摆放,自上而下分别叫第一层、第二层…第n层,第n层的小正方体的个数记为S.解答下列问题:
n | 1 | 2 | 3 | 4 | … |
S | 1 | 3 | … |
(1)按要求填写上表:
(2)研究上表可以发现S随n的变化而变化,且S随n的增大而增大有一定的规律,请你用式子来表示S与n的关系,并计算当n=10时,S的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
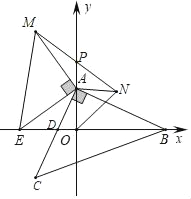
【题目】如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠CAB=90°,点A,点B的坐标分别为A(0,a),B(b,0),且a,b满足a2+b2﹣4a﹣8b+20=0,AC与x轴交于点D.
(1)求△AOB的面积;
(2)求证:点D为AC的中点;
(3)点E为x轴的负半轴上的动点,分别以OA,AE为直角边在第一、二象限作等腰直角三角形△OAN和等腰直角三角形△EAM,连接MN交y轴于点P,试探究线段OE与AP的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场销售某种冰箱,每台进价为2500元,市场调研表明:当每台销售价定为2900元时,平均每天能售出8台;每台售价每降低50元,平均每天能多售出4台.
设该种冰箱每台的销售价降低了x元.
(1)填表:
每天售出的冰箱台数(台) | 每台冰箱的利润(元) | |
降价前 | 8 | |
降价后 |
(2)若商场要想使这种冰箱的销售利润平均每天达到5000元,则每台冰箱的售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550-1617年),纳皮尔发明对数是在指数书写方式之前,直到![]() 世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若
世纪瑞士数学家欧拉(L.Euler,1707-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若![]() ,那么
,那么![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作:
的对数,记作:![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .我们根据对数的定义可得到对数的一个性质:
.我们根据对数的定义可得到对数的一个性质:![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() );理由如下:设
);理由如下:设![]() M=m,
M=m,![]() ,则
,则![]() ,
,![]()
![]() ,由对数的定义得
,由对数的定义得![]() 又
又![]() +
+![]()
![]() .解决一下问题:
.解决一下问题:
(1)将指数式![]() 转化为对数式___________;
转化为对数式___________;
(2)证明![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() );
);
(3)拓展运用:计算![]() =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
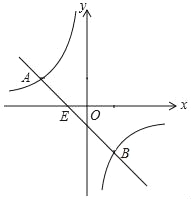
【题目】如图,已知A(﹣4,n),B(4﹣n,﹣4)是直线y=kx+b和双曲线y=![]() 的两个交点.
的两个交点.
(1)求两个函数的表达式;
(2)观察图象,直接写出不等式kx+b﹣![]() ≥0的解集.
≥0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,过点A作AE⊥CD,交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE是⊙O的切线;
(2)已知AE=8cm,CD=12cm,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com