
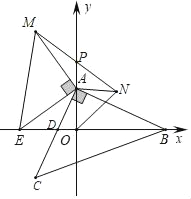
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABCΪ����ֱ�������Σ���CAB��90������A����B������ֱ�ΪA��0��a����B��b��0������a��b����a2+b2��4a��8b+20��0��AC��x�ύ�ڵ�D��
��1������AOB�������
��2����֤����DΪAC���е㣻
��3����EΪx��ĸ������ϵĶ��㣬�ֱ���OA��AEΪֱ�DZ��ڵ�һ��������������ֱ����������OAN�͵���ֱ����������EAM������MN��y���ڵ�P����̽���߶�OE��AP��������ϵ����֤����Ľ��ۣ�
���𰸡���1��4����2������������3����������
��������
��1��a2+b2��4a��8b+20����a��2��2+��b��4��2��0��������⣻
��2���ɡ�ABO����DAO���ý�ֱ�������εķ���������⣻
��3��֤����AHM�ա�EOA��AAS������MPH�ա�NPA��AAS����������⣮
�⣺��1��a2+b2��4a��8b+20����a��2��2+��b��4��2��0��
��a��2��b��4��
S��AOB��![]() OAOB��4��
OAOB��4��
��2����OAB+��OBA��90������OAB+��DAO��90����
���ABO����DAO��
OA��2��OB��4����AB��![]() ��cos��ABO��
��cos��ABO��![]() ��
��![]() ,
,
AD��![]() ��
��![]() ��
��![]() AB��
AB��![]() AC��
AC��
������DΪAC���е㣻
��3������M��MH��y�ύ�ڵ�H��
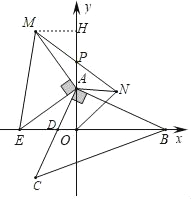
�ߡ�MAH+��EAO��90������MAH+��HMA��90����
���HMA����EAO��
�֡�MHA����AOE��90����AE��AM��
���AHM�ա�EOA��AAS����
��AH��OE��MH��OA��AN��
�֡�MHA����NAP��90������MPH����APN��
���MPH�ա�NPA��AAS����
��AP��PH��![]() AH��
AH��![]() OE��
OE��


 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������˵����
�ٹ�һ������ֻ��һ��ֱ������ֱ֪��ƽ�У�
������t��4��2-3t��1����t����ȡ��ֵ��3����
�۶���ʽ���Ե���ʽ�����Ĵ������ڶ���ʽ�Ĵ����뵥��ʽ�����Ļ�
�ܹ���x��y�ķ�����![]() �����˷���������������������߷ֱ��Ӧ��ӣ��õ�һ���µķ��̣����е�aÿȡһ��ֵʱ������һ�����̣�����Щ��������һ�������⣬�������������
�����˷���������������������߷ֱ��Ӧ��ӣ��õ�һ���µķ��̣����е�aÿȡһ��ֵʱ������һ�����̣�����Щ��������һ�������⣬�������������![]() �����д�����ǣ��� ����
�����д�����ǣ��� ����
A. �ڢۢ�B. �٢ۢ�C. �ڢ�D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶Ϊ1����ABC�ǡ�O���ڽӵȱ������Σ���D��E��Բ�ϣ��ı���BCDEΪ���Σ�������ε�����ǣ� ��
A.2
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
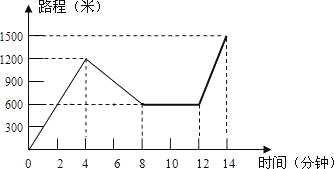
����Ŀ��С��������Ӽ�������ﳵȥ�˾˼����ͣ���������һ��·ʱ������Ҫ������������ܣ��������ۻص��վ�����һ���̵꣬���������ּ����ﳵȥ�˾˼ң�������������ȥ�˾˼����õ�ʱ����·�̵Ĺ�ϵʽʾ��ͼ������ͼ���ṩ����Ϣ�ش��������⣺
(1)С��ҵ��˾˼ҵ�·����______�ף�С�����̵�ͣ����______���ӣ�
(2)������ȥ�˾˼ҵ�;���ĸ�ʱ���С���ﳵ�ٶ���죬�����ٶ��Ƕ�����/��
(3)����ȥ�˾˼ҵ��г��У�С��һ����ʻ�˶����ף�һ�����˶��ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ȵ��Ϊ0.8Ԫ�����õ���Ϊ1�ڶȣ�����ȼƻ�����۵���0.55��0.75֮�䣬�����㣬����۵���xԪ������������õ���y���ڶȣ��루x��0.4����Ԫ���ɷ��������ֵ�x��0.65ʱ��y��0.8������y��x֮��ĺ�����ϵʽ������Ԥ�㣬���ÿ�ȵ�ijɱ���Ϊ0.3Ԫ����۵���0.6Ԫʱ������ȵ������ŵĴ�������_____��Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ������
������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() �ǵ��������Σ���
�ǵ��������Σ���![]() �Ĵ�СΪ_________��.
�Ĵ�СΪ_________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1+��2��180�㣬��3����B����˵��DE��BC�������Dz����Ƶ����̣������������������Ƶ����ݻ����ݣ�
֤�����ߡ�1+��2��180�㣨��֪��
��1����4 ���� ����
���2+��4��180�㣨����������
��EH��AB���� ����
���B���� ������ ����
�ߡ�3����B����֪��
���3����EHC������������
��DE��BC ���� ����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com