
����Ŀ��С��������Ӽ�������ﳵȥ�˾˼����ͣ���������һ��·ʱ������Ҫ������������ܣ��������ۻص��վ�����һ���̵꣬���������ּ����ﳵȥ�˾˼ң�������������ȥ�˾˼����õ�ʱ����·�̵Ĺ�ϵʽʾ��ͼ������ͼ���ṩ����Ϣ�ش��������⣺
(1)С��ҵ��˾˼ҵ�·����______�ף�С�����̵�ͣ����______���ӣ�
(2)������ȥ�˾˼ҵ�;���ĸ�ʱ���С���ﳵ�ٶ���죬�����ٶ��Ƕ�����/��
(3)����ȥ�˾˼ҵ��г��У�С��һ����ʻ�˶����ף�һ�����˶��ٷ��ӣ�
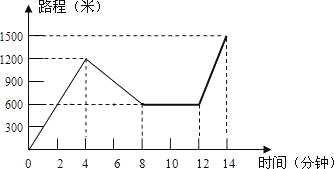
���𰸡�(1)1500��4��(2)С����12��14������죬�ٶ�Ϊ450��/�֣�(3)С�칲��ʻ��2700�ף�������14���ӣ�
��������
��1������ͼ��·�̵����ֵ��ΪС��ҵ��˾˼ҵ�·�̣���ͼ����Ӧ�����ҵ������̵�ͣ����ʱ��Σ������ɵ��������ͣ����ʱ�䣻
��2������ͼ���Һ����仯����һ�Σ��ɵ�С���ﳵ�ٶ�����ʱ��Σ������ɵ����ٶȣ�
��3���ֿ�ʼ��ʻ��·�̣��ۻ��̵���ʻ��·���Լ����̵굽�˾˼���ʻ��·��������Ӽ������С��һ����ʻ·�̣���ͼ������ñ���ȥ�˾˼ҵ��г��У�С��һ���õ�ʱ�䣮
�⣺(1)����ͼ��˾˼�������Ϊ1500��С��ҵ�������Ϊ0����С��ҵ��˾˼ҵ�·����1500�ף������⣬С�����̵�ͣ����ʱ��Ϊ��8�ֵ�12�֣���С�����̵�ͣ����4���ӣ�
�ʴ�Ϊ��1500��4��
(2)����ͼ��12��x��14ʱ��ֱ�����
��С����12��14������죬�ٶ�Ϊ![]() ��450��/�֣�
��450��/�֣�
(3)��ͼ�ɵã�С�칲��ʻ��1200+600+900��2700�ף�������14���ӣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ǿ��Сѧ�������˶���ij�е�ʮ�߽���Сѧ���ᄊ�˶����������������У���������ϯ̨������ͼ��ʾ�������ﶥ��D�뿴̨��A�����ߺ͵��洹ֱ����ö���CD�ij�Ϊ12�ף���BAC=30�㣬��ACD=45�㣬��̨AC�ij������������һλС�����ο����ݣ� ![]() ��1.41��
��1.41�� ![]() ��1.73��
��1.73��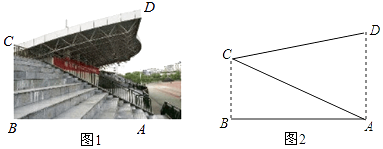
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪AD��AE�ֱ��ǡ�ADC�͡�ABC�ĸߺ����ߣ�AB=6cm��AC=8cm��BC=10cm����CAB=90��������
��1��AD�ij���
��2����ABE�������
��3����ACE�͡�ABE���ܳ��IJ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB=AC����A=100�㣬BDƽ����ABC����֤��BC=BD+AD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=x2��2x+m��ͼ����x���һ������������ǣ���1��0������ͼ����x�����һ������������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
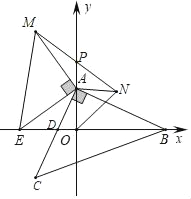
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABCΪ����ֱ�������Σ���CAB��90������A����B������ֱ�ΪA��0��a����B��b��0������a��b����a2+b2��4a��8b+20��0��AC��x�ύ�ڵ�D��
��1������AOB�������
��2����֤����DΪAC���е㣻
��3����EΪx��ĸ������ϵĶ��㣬�ֱ���OA��AEΪֱ�DZ��ڵ�һ��������������ֱ����������OAN�͵���ֱ����������EAM������MN��y���ڵ�P����̽���߶�OE��AP��������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���BD�ϵĵ㣬��1=��2.
��֤����1��BE=DF����2��AF��CE.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ������Ĵ�ʼ�����ո�����ѧ����Ƥ����J.Napier��1550-1617�꣩����Ƥ��������������ָ����д��ʽ֮ǰ��ֱ��![]() ������ʿ��ѧ��ŷ����L.Euler��1707-1783�꣩�ŷ���ָ�������֮�����ϵ.�����Ķ��壺һ��أ���
������ʿ��ѧ��ŷ����L.Euler��1707-1783�꣩�ŷ���ָ�������֮�����ϵ.�����Ķ��壺һ��أ���![]() ����ô
����ô![]() ������
������![]() ��
Ϊ��![]() �Ķ�����������
�Ķ�����������![]() .����ָ��ʽ
.����ָ��ʽ![]() ����ת��Ϊ
����ת��Ϊ![]() ������ʽ
������ʽ![]() ����ת��Ϊ
����ת��Ϊ![]() .���Ǹ��ݶ����Ķ���ɵõ�������һ�����ʣ�
.���Ǹ��ݶ����Ķ���ɵõ�������һ�����ʣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����������£���
�����������£���![]() M=m��
M=m��![]() ����
����![]() ��
��![]()
![]() ���ɶ����Ķ����
���ɶ����Ķ����![]() ��
��![]() +
+![]()
![]() .���һ�����⣺
.���һ�����⣺
��1����ָ��ʽ![]() ת��Ϊ����ʽ___________��
ת��Ϊ����ʽ___________��
��2��֤��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����
��3����չ���ã�����![]() =________.
=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֵĵ���ά��Ҫ��30ǧ��Զ�Ľ������е������ޣ�����������Ħ�г����ߣ�15���Ӻ�����װ����������ϳ������������ͬʱ�����֪�������ٶ���Ħ�г���1.5�����������ֳ����ٶȣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com