
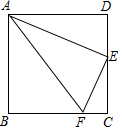
 如图,边长为2的正方形ABCD中,E、F分别是BC、CD上的点(E、F与顶点不重合),∠AFD=90°.
如图,边长为2的正方形ABCD中,E、F分别是BC、CD上的点(E、F与顶点不重合),∠AFD=90°.分析 (1)由正方形的性质和角的互余关系即可得出结论;
(2)由相似三角形的性质得出对应边成比例,即可得出y与x的函数关系式,化成顶点式,即可得出y的最小值.
解答 (1)证明:如图所示: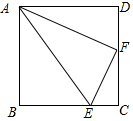
∵四边形ABCD是正方形,
∴∠D=∠C=90°,
∴∠DAF+∠AFD=90°,
∵∠AFE=90°,
∴∠AFD+∠CFE=90°,
∴∠DAF=∠CFE,
∴△ADF∽△FCE;
(2)解:∵△ADF∽△FCE,
∴$\frac{AD}{FC}=\frac{DF}{CE}$,即$\frac{2}{x}=\frac{2-x}{2-y}$,
整理得:y=$\frac{1}{2}$x2-x+2,
即y与x的函数关系式为y=$\frac{1}{2}$x2-x+2,
∵y=$\frac{1}{2}$x2-x+2=$\frac{1}{2}$(x-1)2+$\frac{3}{2}$,$\frac{1}{2}$>0,
∴y的最小值为$\frac{3}{2}$.
点评 本题考查了正方形的性质、相似三角形的判定与性质、二次函数的性质;熟练掌握正方形的性质,证明三角形相似是解决问题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 候选人 | 教学技能考核成绩 | 专业知识考核成绩 |
| 甲 | 85 | 92 |
| 乙 | 91 | 85 |
| 丙 | 80 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
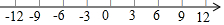 动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4 (速度单位:单位长度/秒).
动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4 (速度单位:单位长度/秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形的内心到三角形三个顶点的距离相等 | |
| B. | 三角形的内心不一定在三角形的内部 | |
| C. | 等边三角形的内心,外心重合 | |
| D. | 一个圆一定有唯一一个外切三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com