
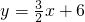 的值分别满足下列条件:
的值分别满足下列条件: 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2008年湖北省仙桃市(潜江 江汉 油田)初中毕业升学统一考试、数学试卷 题型:044
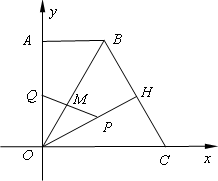
如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2,2![]() ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
(1)求OH的长;
(2)若△OPQ的面积为S(平方单位).求S与t之间的函数关系式.并求t为何值时,△OPQ的面积最大,最大值是多少?
(3)设PQ与OB交于点M.①当△OPM为等腰三角形时,求(2)中S的值.
②探究线段OM长度的最大值是多少,直接写出结论.
查看答案和解析>>
科目:初中数学 来源:2007年江苏地区数学中考动态型试题-新人教 题型:059
已知:如下图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为t(秒).
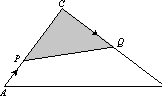
(1)当时间t为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间t的函数关系式,并指出自变量t的取值范围;
(3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com