
【题目】已知关于x的一元二次方程x2﹣3x﹣![]() k2+k+1=0.
k2+k+1=0.
(1)证明:原方程有两个不相等的实数根;
(2)若原方程的两实根分别为x1,x2,且(x1﹣x2+2)(x1﹣x2﹣2)=﹣3,求k的值.
【答案】(1)见解析;(2)k的值为2.
【解析】
(1)计算判别式得到△=(k-2)2+1,利用非负数的性质得到△>0,从而得到结论;
(2)利用根与系数的关系得到x1+x2=3、x1x2=![]() ,再变形已知条件得到(x1+x2)2-4x1x2-1=0,即
,再变形已知条件得到(x1+x2)2-4x1x2-1=0,即![]() ,然后解关于k的不等式即可.
,然后解关于k的不等式即可.
(1)证明:∵△=(﹣3)2﹣4(﹣![]() k2+k+1)
k2+k+1)
=k2﹣4k+5
=(k﹣2)2+1,
∵(k﹣2)2≥0,
∴(k﹣2)2+1>0,即△>0,
∴无论k取何值,该方程总有两个不相等的实数根;
(2)解:根据题意得x1+x2=3、x1x2=﹣![]() k2+k+1,
k2+k+1,
∵(x1﹣x2+2)(x1﹣x2﹣2)=﹣3,
∴(x1﹣x2)2﹣4=﹣3,
(x1+x2)2﹣4x1x2﹣1=0,
即32﹣4(﹣![]() k2+k+1)﹣1=0,
k2+k+1)﹣1=0,
整理得k2﹣4k+4=0,解得k1=k2=2,
即k的值为2.


科目:初中数学 来源: 题型:
【题目】飞机着陆后滑行的距离y(单位:m)关于滑行时间以(单位:)的函数解析式是y=6t﹣![]() t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
t2.在飞机着陆滑行中,滑行最后的150m所用的时间是( )s.
A.10B.20C.30D.10或30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图平面直角坐标系中,直线y=kx+1与x轴交于点A点,与y轴交于B点,P(a,b)是这条直线上一点,且a、b(a<b)是方程x2﹣6x+8=0的两根.Q是x轴上一动点,N是坐标平面内一点,以点P、B、Q、N四点为顶点的四边形恰好是矩形,则点N的坐标为_____或_____.
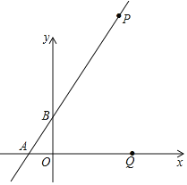
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的顶点为B(1,3),与
的顶点为B(1,3),与![]() 轴的交点A在点 (2,0)和(3,0)之间.以下结论:
轴的交点A在点 (2,0)和(3,0)之间.以下结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ≥
≥![]() ;⑤若
;⑤若![]() ,且
,且![]() ,
,
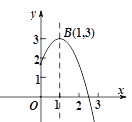
则![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)求该函数图象与x轴,y轴的交点坐标以及它的顶点坐标:
(2)根据(1)的结果在坐标系中利用描点法画出此抛物线.
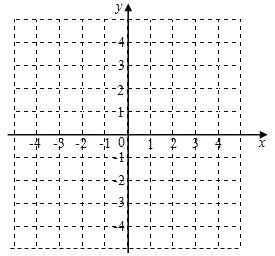
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,![]() 的两边分别与AB,BC交于点E,F,与对角线AC交于点G,H,已知
的两边分别与AB,BC交于点E,F,与对角线AC交于点G,H,已知![]() ,
,![]() .
.
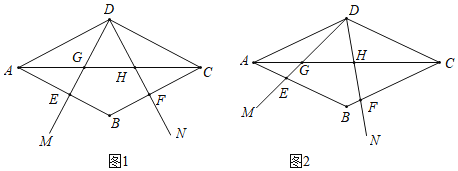
(1)如图1,当![]() ,
,![]() 时,
时,
①求证:![]() ;
;
②求线段GH的长;
(2)如图2,当![]() 绕点D旋转时,线段AG,GH,HC的长度都在变化.设线段
绕点D旋转时,线段AG,GH,HC的长度都在变化.设线段![]() ,
,![]() ,
,![]() ,试探究p与mn的等量关系,并说明理由.
,试探究p与mn的等量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com