
【题目】在菱形ABCD中,![]() 的两边分别与AB,BC交于点E,F,与对角线AC交于点G,H,已知
的两边分别与AB,BC交于点E,F,与对角线AC交于点G,H,已知![]() ,
,![]() .
.
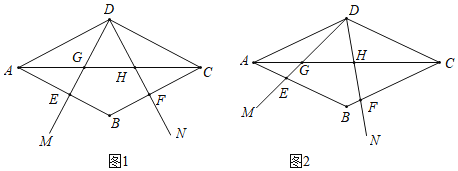
(1)如图1,当![]() ,
,![]() 时,
时,
①求证:![]() ;
;
②求线段GH的长;
(2)如图2,当![]() 绕点D旋转时,线段AG,GH,HC的长度都在变化.设线段
绕点D旋转时,线段AG,GH,HC的长度都在变化.设线段![]() ,
,![]() ,
,![]() ,试探究p与mn的等量关系,并说明理由.
,试探究p与mn的等量关系,并说明理由.
【答案】(1)①详见解析;②2;(2)![]()
【解析】
(1)①利用AAS直接得出结论;
②先判断出![]() ,
,![]() ,证明
,证明![]() 是等边三角形,进而求出
是等边三角形,进而求出![]() ,即可得出结论;
,即可得出结论;
(2)先判断出C'G=CH=p,再求出AP=![]() m,PG=
m,PG=![]() m,进而得出PC'=n
m,进而得出PC'=n![]() m,进而得出p2=(n
m,进而得出p2=(n![]() m)2+(
m)2+(![]() m)2①,再判断出m+n+p=6②,联立即可得出结论.
m)2①,再判断出m+n+p=6②,联立即可得出结论.
(1)①证明:∵![]() ,
,![]() ,
,
∴![]()
∵在菱形ABCD中,![]() ,
,![]() ,
,
∴![]() ;
;
②解:∵在菱形ABCD中,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,/span>
,/span>
∴![]() ,
,
同理![]() ,
,
∵![]() ,
,![]() ,
,
∵![]()
∴![]() 是等边三角形,即
是等边三角形,即![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:p与mn的等量关系是:![]() .
.
理由:将![]() 绕点D顺时针旋转
绕点D顺时针旋转![]() 得到
得到![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
连接KG,作![]() 于点R,
于点R,
则![]() ,
,
![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴在![]() 中,
中,![]() ,即
,即 ,
,
整理得:![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,化简得
,化简得![]() .
.
因此所求的等量关系式是:![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】2019年九龙口诗词大会在九龙口镇召开,我校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作.本次学生志愿者工作一共设置了三个岗位,分别是引导员、联络员和咨询员.
(1)若要从这5名志愿者中随机选取一位作为引导员,求选到女生的概率;
(2)若甲、乙两位志愿者都从三个岗位中随机选择一个,请你用画树状图或列表法求出他们恰好选择同一个岗位的概率.(画树状图和列表时可用字母代替岗位名称)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣3x﹣![]() k2+k+1=0.
k2+k+1=0.
(1)证明:原方程有两个不相等的实数根;
(2)若原方程的两实根分别为x1,x2,且(x1﹣x2+2)(x1﹣x2﹣2)=﹣3,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
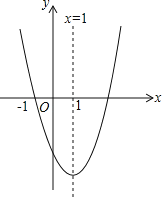
【题目】如图抛物线y=ax2+bx+c的图象经过(﹣1,0),对称轴x=1,则下列三个结论:①abc<0;②10a+3b+c>0;③am2+bm+a≥0.正确的结论为_____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市连续5天的天气情况.

(1)利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大;
(2)根据如图提供的信息,请再写出两个不同类型的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,BC∥AD,∠B=90°,AD边落在平面直角坐标系的x轴上,且点A(5,0)、C(0,3)、AD=2.点P从点E(﹣5,0)出发,沿x轴向点A以每秒1个单位长度的速度运动,到达点A时停止运动.运动时间为t秒.
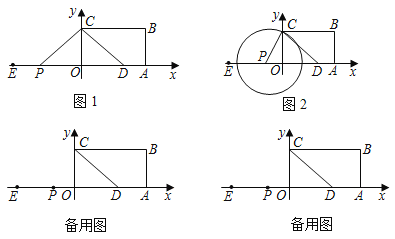
(1)∠BCD的度数为______°.
(2)当t=_____时,△PCD为等腰三角形.
(3)如图2,以点P为圆心,PC为半径作⊙P.
①求当t为何值时,⊙P与四边形ABCD的一边(或边所在的直线)相切.
②当t______时,⊙P与四边形ABCD的交点有两个;当t_____时,⊙P与四边形ABCD的交点有三个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
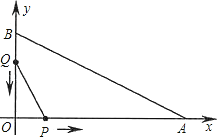
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,山上有一座高塔,山脚下有一圆柱形建筑物平台,高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上,在点A处测得塔顶H的仰角为35°,在点D处测得塔顶H的仰角为45°,又测得圆柱形建筑物的上底面直径AD为6m,高CD为2.8m,则塔顶端H到地面的高度HG为( )
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
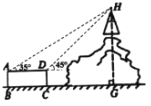
A.10.8mB.14mC.16.8mD.29.8m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com