

分析 (1)作点B关于AM的对称点E,连结AE,ED,EM,通过证明△ABM≌△AEM,△EMD≌△CMD证得AE=AB,ED=CD,最后通过三角形三关系证得AB+CD>AD.
(2)根据对称性,作出点B关于AM的对称点B′,点C关于MD的对称点C′,再连接AB′、B′C′、C′D、B′M、C′M,根据轴对称的性质以及∠AMD=120°可以证明△B′C′M是等边三角形,然后根据连接两点的所有线中,线段最短证明.
(3)通过(2)的分析得到∠B′MC′=90°,在等腰Rt△B′MC′中,求得B′C′=2,最后由AD≤AB′+B′C′+C′D求得AD的最大值.
解答 解:(1)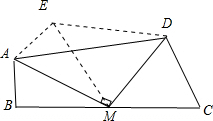 如右图,作点B关于AM的对称点E,连结AE,ED,EM,根据轴对称的性质,可得AE=AB,EM=BM,∠AEM=∠B,
如右图,作点B关于AM的对称点E,连结AE,ED,EM,根据轴对称的性质,可得AE=AB,EM=BM,∠AEM=∠B,
∴△AEM≌△ABM,
∴∠ABM=∠AME,
∵∠AMD=90°,
∴∠AMB+∠DMC=180-∠AMD=180°-90°=90°,
∵∠AME+∠EMD=90°,
∴∠EMD=∠DMC,
∵BM=MC=ME,DM=DM,
∴△EMD≌△CMD,
∴ED=DC,
∵AE+ED>AD,
∴AB+CD>AD,
(2)证明:如右图,作出点B关于AM的对称点B′,点C关于MD的对称点C′,连接AB′、B′C′、C′D、B′M、C′M,
根据轴对称的性质可得AB′=AB,BM=B′M,CM=C′M,C′D=CD,∠AMB=AMB′,∠DMC=∠DMC′,
∵∠AMD=120°,
∴∠AMB+∠DMC=180°-∠AMD=180°-120°=60°,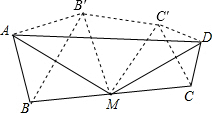
∴∠B′MC′=∠AMD-(∠AMB′+∠DMC′)=120°-60°=60°,
∵点M是四边形ABCD的边BC的中点,
∴BM=CM,
∴B′M=C′M,
∴△B′C′M是等边三角形,
∴B′C′=$\frac{1}{2}$BC,
所有,①当点B′、C′在AD上时,AB+$\frac{1}{2}$BC+CD=AD,
②当点B′、C′不在AD上时,根据连接两点的所有线中,线段最短,AB+$\frac{1}{2}$BC+CD>AD,
综上,AB+$\frac{1}{2}$BC+CD≥AD.
(3)由(2)知当∠AMD=135°时,∠B′MC′=90°,
在Rt△B′MC′中,B′M=MC′=$\frac{1}{2}$BC=$\frac{1}{2}$×$2\sqrt{2}$=$\sqrt{2}$,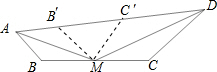
∴B′C′=$\sqrt{{B}^{′}{M}^{2}+{C}^{′}{M}^{2}}$=2
又∵A′B=AB=1,C′D=CD=2,
∴AD≤AB′+B′C′+C′D=1+2+2=5,
∴AD的最大值是5.
点评 本题考查了轴对称的性质,两点间线段最短的性质,作出对称点构造出图形更形象直观,注意证明得到(2)△B′C′M是等边三角形,(3)中△B′C′M是等腰直角三角形非常关键


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 正比例 | B. | 反比例 | C. | 不成比例 | D. | 一次函数关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
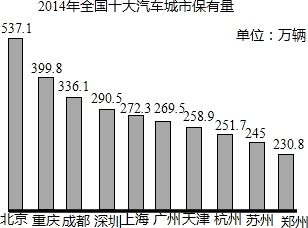 2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.
2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 考试分数(分) | 20 | 16 | 12 | 8 |
| 人数 | 24 | 18 | 5 | 3 |
| A. | 20,16 | B. | l6,20 | C. | 20,l2 | D. | 16,l2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一转盘被平均分成8份,转动指针,停止后指针指向的数字即为转出的数字.现有两种规则:规则A:甲方猜“是正数”,乙方猜“是负数”;规则B:甲方猜“是负整数”,乙方猜“是分数”;请问哪个规则公平?规则A和规则B.
如图,一转盘被平均分成8份,转动指针,停止后指针指向的数字即为转出的数字.现有两种规则:规则A:甲方猜“是正数”,乙方猜“是负数”;规则B:甲方猜“是负整数”,乙方猜“是分数”;请问哪个规则公平?规则A和规则B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com