练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．平面上有2004条直线，且任何两条不平行，任何三条不共点，则它们彼此相交而成的线段有（　　）
    A．2003×2002×1002B．2003×2002×2004C．2004×2003×1002D．2004×2003×2004

    分析 直接由组合的概念求出2004条直线共形成交点的组合数，即可得到结论．

    解答 解：∵平面上有2004条直线，且任何两条不平行，任何三条不共点，
    ∵每一条直线与另外2003条直线由2003个交点，每一个交点与剩下的2002个交点都组成一条线段，但线段AB与线段BA是同一条线段，所有线段都重复计算了两遍，
    ∴它们彼此相交而成的线段有2004×$\frac{2003×2002}{2}$=2004×2003×1002条，
    故选C．

    点评 本题考查了平行线的性质，正确的理解题意是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．若x=$\sqrt{2}$a是不等式组$\left\{\begin{array}{l}{x+3≥0}\\{2（x-1）+3≥3x}\end{array}\right.$的解，则a的取值范围是-$\frac{3\sqrt{2}}{2}$≤a≤$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

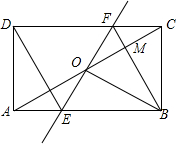    12．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中一定成立的结论有①③④（将正确结论的序号填在横线上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

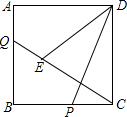    9．如图，四边形ABCD为正方形，AD=3，点P、点Q分别是BC、AB边上的动点，CP=AQ，连接DP、CQ，在线段CQ上有一动点E，满足∠DEC=∠DPC，则CE•CQ的值为9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．-26，-6，2，4，6，（　　）
    A．11B．12C．13D．14

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在△ABC中，DE∥BC，若$\frac{AD}{DB}$=$\frac{2}{3}$，则$\frac{AE}{EC}$=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．随着出行方式的多样化，某地区三类打车方式的收费标准如下：
    出租车滴滴打车神州打车
    3千米以内：12元1.5元/千米2元/千米
    超过3千米的部分：2.4元/千米0.5元/分钟0.6元/分钟
    （如：乘坐8千米，耗时12分钟，出租车的收费为：12+2.4×（8-3）=24（元）；滴滴打车的收费为：8×1.5+12×0.5=18（元）；神州打车的收费为：8×2+12×0.6=23.2（元））
    解决问题：（假设打车的平均车速为30千米/小时）
    （1）小明乘车从新街口去南京南站，全程10千米，如果小明使用滴滴打车，需要支付的打车费用为25；
    （2）小红乘车从南京博物院去南京青奥公园，用滴滴打车比乘坐出租车节省了3元．求南京博物院到南京青奥公园的路程；
    （3）神州打车为了和滴滴打车竞争客户，分别推出了优惠方式，滴滴打车对于乘车路程在5千米以上（含5千米）的客户每次收费立减9元；神舟打车车费5折优惠．对采用哪一种打车方式更合算提出你的建议．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．在三角形ABC和三角形DEF中，∠B=∠E，要使△ABC∽△DEF，需要补充一个条件是$\frac{AB}{DE}=\frac{BC}{EF}$（写一个即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．先化简再求值：（2a2b-ab2）-2（a2b-ab2），其中a=2，b=-$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案