
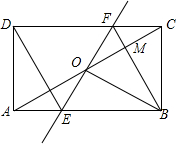
 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上) 分析 ①正确.只要证明BO=BC,OF=FO即可解决问题;
②错误.可以证明△EOB≌△FCB,由此即可判断;
③正确.只要证明△DEF是等边三角形即可.
④正确.只要证明S△BCM=$\frac{1}{4}$S△ACB,S△AOE=$\frac{1}{3}$S△AOB=$\frac{1}{6}$S△ABC即可;
解答 解:∵四边形ABCD是矩形,
∴∠ABC=∠DCB=90°,OA=OC,
∴OB=OA=OB,
∵∠COB=60°,
∴△BOC是等边三角形,
∴∠OCB=60°,
∴∠DCA=30°,
∵FO=FC,BO=BC,
∴BF垂直平分OC,故①正确,
∴∠FBC=∠OBE=30°,
∴∠FOC=∠FCO=30°,
∴∠FOB=90°,
∵CD∥AB,
∴∠FCO=∠EAO,
∵∠FOC=∠AOE,OA=OC,
∴△FOC≌△EOA,
∴OE=OF,
∴BF=BE,∵∠BOE=∠BCF=90°,∠EBO=∠CBF,
∴△EBO≌△FBC,故②错误,
∵DF∥EB,DF=BE,
∴四边形DEBF是平行四边形,
∴∠EDF=∠FBE=60°,∵∠DFE=180°-∠CFO=60°,
∴△EDF是等边三角形,
∴DE=EF,故③正确,
易知CM=$\frac{1}{4}$AC,AE=CF=$\frac{1}{2}$BF=$\frac{1}{2}$BE,
∴S△BCM=$\frac{1}{4}$S△ACB,S△AOE=$\frac{1}{3}$S△AOB=$\frac{1}{6}$S△ABC,
∴S△AOE:S△BCM=2:3.故④正确,
故答案为①③④
点评 本题考查矩形的性质、全等三角形的判定和性质、等边三角形的判定和性质、线段的垂直平分线的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
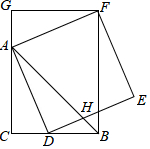 如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论:
如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,以AD为边作正方形ADEF,过点F作FG⊥CA交CA的延长线于点G,连接FB交DE于点H,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2003×2002×1002 | B. | 2003×2002×2004 | C. | 2004×2003×1002 | D. | 2004×2003×2004 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com