
分析 根据a-$\frac{1}{a}$=$\sqrt{7}$,应用完全平方公式,求出a2+$\frac{1}{{a}^{2}}$的值,即可求出a+$\frac{1}{a}$的值是多少.
解答 解:∵a-$\frac{1}{a}$=$\sqrt{7}$,
∴${(a-\frac{1}{a})}^{2}$=7,
∴a2+$\frac{1}{{a}^{2}}$-2=7,
∴a2+$\frac{1}{{a}^{2}}$=9,
∴${(a+\frac{1}{a})}^{2}$=9+2=11,
∵a>0,
∴a+$\frac{1}{a}$>0,
∴a+$\frac{1}{a}$=$\sqrt{11}$.
故答案为:$\sqrt{11}$.
点评 此题主要考查了二次根式的化简求值问题,要熟练掌握,注意完全平方公式的应用.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
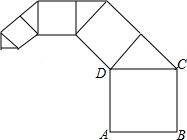 如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为1,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…,按照此规律继续下去,则S2017的值为( )| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
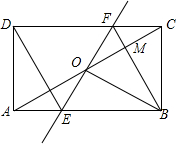 如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)
如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中一定成立的结论有①③④(将正确结论的序号填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
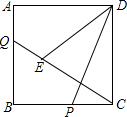 如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9.
如图,四边形ABCD为正方形,AD=3,点P、点Q分别是BC、AB边上的动点,CP=AQ,连接DP、CQ,在线段CQ上有一动点E,满足∠DEC=∠DPC,则CE•CQ的值为9.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com