Question

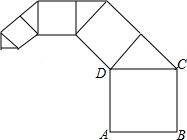
15．如图，正方形ABCD的边长为1，其面积标记为S₁，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S₂，…，按照此规律继续下去，则S₂₀₁₇的值为（　　）

• A． $\frac{1}{{2}^{2014}}$
• B． $\frac{1}{{2}^{2015}}$
• C． $\frac{1}{{2}^{2016}}$
• D． $\frac{1}{{2}^{2017}}$

Answer 1

分析 根据等腰直角三角形的性质可得出2S₂=S₁，写出部分S_n的值，根据数的变化找出变化规律S_n=（$\frac{1}{2}$）^n-1，依此规律即可得出结论．

解答 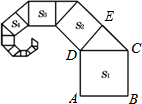解：如图，∵正方形ABCD的边长为1，△CDE为等腰直角三角形，
∴DE²+CE²=CD²，DE=CE，
∴2S₂=S₁．
观察，发现规律：
S₁=1²=1，S₂=$\frac{1}{2}$S₁=$\frac{1}{2}$，S₃=$\frac{1}{2}$S₂=$\frac{1}{4}$，S₄=$\frac{1}{2}$S₃=$\frac{1}{8}$，…，
∴S_n=（$\frac{1}{2}$）^n-1．
当n=2017时，S₂₀₁₇=（$\frac{1}{2}$）^2017-1=（$\frac{1}{2}$）²⁰¹⁶=$\frac{1}{{2}^{2016}}$，
故选：C．

点评 本题考查了等腰直角三角形的性质、勾股定理，解题的关键是找出规律S_n=（$\frac{1}{2}$）^n-1．解决该题型题目时，写出部分S_n的值，根据数值的变化找出变化规律是关键．