
ЁОЬтФПЁПвбжЊЃЌжБЯпABЁЮDCЃЌЕуPЮЊЦНУцЩЯвЛЕуЃЌСЌНгAPгыCPЃЎ
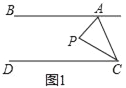
ЃЈ1ЃЉШчЭМ1ЃЌЕуPдкжБЯпABЁЂCDжЎМфЃЌЕБЁЯBAP=60ЁуЃЌЁЯDCP=20ЁуЪБЃЌЧѓЁЯAPCЃЎ
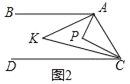
ЃЈ2ЃЉШчЭМ2ЃЌЕуPдкжБЯпABЁЂCDжЎМфЃЌЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌаДГіЁЯAKCгыЁЯAPCжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
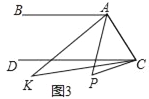
ЃЈ3ЃЉШчЭМ3ЃЌЕуPТфдкCDЭтЃЌЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌЁЯAKCгыЁЯAPCгаКЮЪ§СПЙиЯЕЃПВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ80ЁуЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉМћНтЮі
ЁОНтЮіЁПећЬхЗжЮіЃК
ЗжБ№Й§ЕуPЃЌKзїABЕФЦНааЯпЃЌРћгУЦНааЯпЕФаджЪКЭНЧЦНЗжЯпЕФЖЈвхМДПЩЧѓНт.
НтЃКЃЈ1ЃЉШчЭМ1ЃЌЙ§PзїPEЁЮABЃЌ
ЁпABЁЮCDЃЌ
ЁрPEЁЮABЁЮCDЃЌ
ЁрЁЯAPE=ЁЯBAPЃЌЁЯCPE=ЁЯDCPЃЌ
ЁрЁЯAPC=ЁЯAPE+ЁЯCPE=ЁЯBAP+ЁЯDCP=60Ёу+20Ёу=80ЁуЃЛ
ЃЈ2ЃЉЁЯAKC=![]() ЁЯAPCЃЎ
ЁЯAPCЃЎ
РэгЩЃКШчЭМ2ЃЌЙ§KзїKEЁЮABЃЌ
ЁпABЁЮCDЃЌ
ЁрKEЁЮABЁЮCDЃЌ
ЁрЁЯAKE=ЁЯBAKЃЌЁЯCKE=ЁЯDCKЃЌ
ЁрЁЯAKC=ЁЯAKE+ЁЯCKE=ЁЯBAK+ЁЯDCKЃЌ
Й§PзїPFЁЮABЃЌ
ЭЌРэПЩЕУЃЌЁЯAPC=ЁЯBAP+ЁЯDCPЃЌ
ЁпЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌ
ЁрЁЯBAK+ЁЯDCK=![]() ЁЯBAP+
ЁЯBAP+![]() ЁЯDCP=
ЁЯDCP=![]() ЃЈЁЯBAP+ЁЯDCPЃЉ=
ЃЈЁЯBAP+ЁЯDCPЃЉ=![]() ЁЯAPCЃЌ
ЁЯAPCЃЌ
ЁрЁЯAKC=![]() ЁЯAPCЃЛ
ЁЯAPCЃЛ
ЃЈ3ЃЉЁЯAKC=![]() ЁЯAPCЃЎ
ЁЯAPCЃЎ
РэгЩЃКШчЭМ3ЃЌЙ§KзїKEЁЮABЃЌ
ЁпABЁЮCDЃЌ
ЁрKEЁЮABЁЮCDЃЌ
ЁрЁЯBAK=ЁЯAKEЃЌЁЯDCK=ЁЯCKEЃЌ
ЁрЁЯAKC=ЁЯAKEЉЁЯCKE=ЁЯBAKЉЁЯDCKЃЌ
Й§PзїPFЁЮABЃЌ
ЭЌРэПЩЕУЃЌЁЯAPC=ЁЯBAPЉЁЯDCPЃЌ
ЁпЁЯBAPгыЁЯDCPЕФНЧЦНЗжЯпЯрНЛгкЕуKЃЌ
ЁрЁЯBAKЉЁЯDCK=![]() ЁЯBAPЉ
ЁЯBAPЉ![]() ЁЯDCP=
ЁЯDCP=![]() ЃЈЁЯBAPЉЁЯDCPЃЉ=
ЃЈЁЯBAPЉЁЯDCPЃЉ=![]() ЁЯAPCЃЌ
ЁЯAPCЃЌ
ЁрЁЯAKC=![]() ЁЯAPCЃЎ
ЁЯAPCЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛзщЪ§ОнЙВ50ИіЃЌЗжЮЊ6зщЃЌЕквЛзщЕФЦЕЪ§ЮЊ5ЃЌЕкЖўзщЕФЦЕЪ§ЮЊ7ЃЌЕкШ§зщЕФЦЕЪ§ЮЊ8ЃЌЕкЫФзщЕФЦЕЪ§ЮЊ10ЃЌЕкЮхзщЕФЦЕТЪЪЧ0.2ЃЌдђЕкСљзщЕФЦЕЪ§ЪЧ( )
A. 10 B. 0.2 C. 40 D. 8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
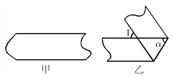
ЁОЬтФПЁПЃЈ1ЃЉгавЛЬѕжНДјШчЭММзЫљЪОЃЌдѕбљМьбщжНДјЕФСНЬѕБпЯпЪЧЗёЦНааЃПЫЕУїФуЕФЗНЗЈКЭРэгЩЃЎ
ЃЈ2ЃЉШчЭМввЃЌНЋвЛЬѕЩЯЯТСНБпЛЅЯрЦНааЕФжНДјелЕўЃЌЩшЁЯ1ЮЊxЖШЃЌЧыгУxЕФДњЪ§ЪНБэЪОЁЯІСЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЪЧЪРНчЩЯбЯжиШБЫЎЕФЙњМвжЎвЛЃЎЮЊСЫдіЧПОгУёЕФНкЫЎвтЪЖЃЌФГЪаздРДЫЎЙЋЫОЖдОгУёгУЫЎВЩгУвдЛЇЮЊЕЅЮЛЗжЖЮМЦЗбЕФАьЗЈЪеЗбЃЎМДвЛИідТгУЫЎ10ЖжвдФкЃЈАќРЈ10ЖжЃЉЕФгУЛЇЃЌУПЖжЪеЫЎЗбaдЊЃЛвЛИідТгУЫЎГЌЙ§10ЖжЕФгУЛЇЃЌ10ЖжЫЎШдАДУПЖжaдЊЪеЗбЃЌГЌЙ§10ЖжЕФВПЗжЃЌАДУПЖжbдЊЃЈbЃОaЃЉЪеЗбЃЎЩшвЛЛЇОгУёдТгУЫЎxЖжЃЌгІЪеЫЎЗбyдЊЃЌyгыxжЎМфЕФКЏЪ§ЙиЯЕШчЭМ
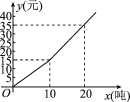
ЃЈ1ЃЉЧѓaЕФжЕЃЌФГЛЇОгУёЩЯдТгУЫЎ8ЖжЃЌгІЪеЫЎЗбЖрЩйдЊЃЛ
ЃЈ2ЃЉЧѓbЕФжЕЃЌВЂаДГіЕБxЃО10ЪБЃЌyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП3дТЮоЮ§ЪаЩЬЦЗЗПЦНОљУПЦНЗНМлИёЮЊ7500дЊЃЌ7500дЊгУПЦбЇМЧЪ§ЗЈБэЪОЮЊдЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊmЪЧвЛдЊЖўДЮЗНГЬx2+xЃН5ЕФЪЕЪ§ИљЃЌЧѓДњЪ§ЪНЃЈ2mЉ1ЃЉЃЈ2m+1ЃЉЉmЃЈmЉ3ЃЉЉ7ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
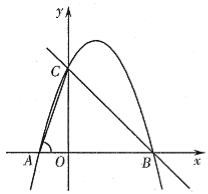
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌжБЯпy=Љx+nгыxжсЁЂyжсЗжБ№НЛгкBЁЂCСНЕуЃЌХзЮяЯпy=ax2+bx+3(aЁй0)Й§CЁЂBСНЕуЃЌНЛxжсгкСэвЛЕуAЃЌСЌНгACЃЌЧвtanЁЯCAO=3ЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНЃЛ
(2)ШєЕуPЪЧЩфЯпCBЩЯвЛЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌДЙзуЮЊHЃЌНЛХзЮяЯпгкQЃЌЩшPЕуКсзјБъЮЊtЃЌЯпЖЮPQЕФГЄЮЊdЃЌЧѓГіdгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІЕФздБфСПtЕФШЁжЕЗЖЮЇЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌЕБЕуPдкЯпЖЮBCЩЯЪБЃЌЩшPH=eЃЌвбжЊdЃЌeЪЧвдyЮЊЮДжЊЪ§ЕФвЛдЊЖўДЮЗНГЬЃКy2Ѓ(m+3)y+![]() (5m2Ѓ2m+13)=0 (mЮЊГЃЪ§)ЕФСНИіЪЕЪ§ИљЃЌЕуMдкХзЮяЯпЩЯЃЌСЌНгMQЁЂMHЁЂPMЃЌЧвЃЎMPЦНЗжЁЯQMHЃЌЧѓГіtжЕМАЕуMЕФзјБъЃЎ
(5m2Ѓ2m+13)=0 (mЮЊГЃЪ§)ЕФСНИіЪЕЪ§ИљЃЌЕуMдкХзЮяЯпЩЯЃЌСЌНгMQЁЂMHЁЂPMЃЌЧвЃЎMPЦНЗжЁЯQMHЃЌЧѓГіtжЕМАЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
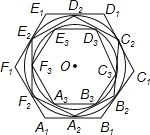
ЁОЬтФПЁПШчЭМЃЌе§СљБпаЮA1B1C1D1E1F1ЕФБпГЄЮЊ2ЃЌе§СљБпаЮA2B2C2D2E2F2ЕФЭтНгдВгые§СљБпаЮA1B1C1D1E1F1ЕФИїБпЯрЧаЃЌе§СљБпаЮA3B3C3D3E3F3ЕФЭтНгдВгые§СљБпаЮA2B2C2D2E2F2ЕФИїБпЯрЧаЃЌЁАДетбљЕФЙцТЩНјааЯТШЅЃЌA10B10C10D10E10F10ЕФБпГЄЮЊЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com