
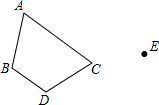
 请画出将四边形ABDC进行平移后,使A到E处的四边形EFGH.
请画出将四边形ABDC进行平移后,使A到E处的四边形EFGH. 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
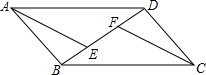 如图:四边形ABCD中AB=DC,AD=BC,点E、F在线段BD上,且BE=DF.(1)求证:△ABD≌△CDB;
如图:四边形ABCD中AB=DC,AD=BC,点E、F在线段BD上,且BE=DF.(1)求证:△ABD≌△CDB; 查看答案和解析>>
科目:初中数学 来源:2013届四川省德阳中学九年级第一次月考数学试卷(带解析) 题型:填空题
操作探究:
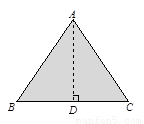
(1)现有一块等腰三角形纸板,量得周长为32cm,底比一腰多2cm.若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请画出你能拼成的各种四边形的示意图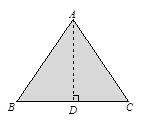
(2)计算拼成的各个四边形的两条对角线长的和.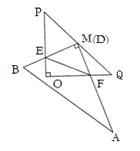
(3)另用纸片制作一个直角边为4的等腰Rt△OPQ,将(1)中的剪得的Rt△ABD纸片的直角顶点D和PQ的中点M重合(如图所示),以M为旋转中心,旋转Rt△ABD纸片,Rt△ABD纸片的两直角边与⊿POQ的两直角边分别交于点E、F. 连接EF,探究:在旋转三角形纸板的过程中,△EOF的周长是否存在最小值,若存在,求出最小值,若不存在。请说明理由。
查看答案和解析>>
科目:初中数学 来源:2012-2013学年四川省九年级第一次月考数学试卷(解析版) 题型:填空题
操作探究:
(1)现有一块等腰三角形纸板,量得周长为32cm,底比一腰多2cm.若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请画出你能拼成的各种四边形的示意图
(2)计算拼成的各个四边形的两条对角线长的和.
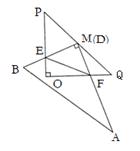
(3)另用纸片制作一个直角边为4的等腰Rt△OPQ,将(1)中的剪得的Rt△ABD纸片的直角顶点D和PQ的中点M重合(如图所示),以M为旋转中心,旋转Rt△ABD纸片,Rt△ABD纸片的两直角边与⊿POQ的两直角边分别交于点E、F. 连接EF,探究:在旋转三角形纸板的过程中,△EOF的周长是否存在最小值,若存在,求出最小值,若不存在。请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
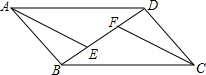 如图:四边形ABCD中AB=DC,AD=BC,点E、F在线段BD上,且BE=DF
如图:四边形ABCD中AB=DC,AD=BC,点E、F在线段BD上,且BE=DF
(1)求证:△ABD≌△CDB;
(2)指出线段AE与CF的关系,并说明理由.
(3)若将题中的条件“点E、F在线段BD上”改为“点E、F在直线BD上”那么你在(2)中得出的结论还一定能成立吗?若能,直接写出结论;若不能,请画出一个图形作为反例说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com