
操作探究:
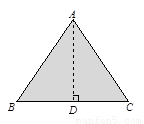
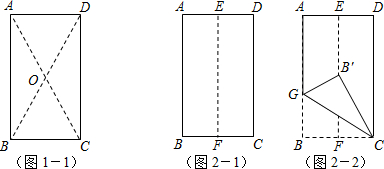
(1)现有一块等腰三角形纸板,量得周长为32cm,底比一腰多2cm.若把这个三角形纸板沿其对称轴剪开,拼成一个四边形,请画出你能拼成的各种四边形的示意图
(2)计算拼成的各个四边形的两条对角线长的和.
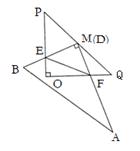
(3)另用纸片制作一个直角边为4的等腰Rt△OPQ,将(1)中的剪得的Rt△ABD纸片的直角顶点D和PQ的中点M重合(如图所示),以M为旋转中心,旋转Rt△ABD纸片,Rt△ABD纸片的两直角边与⊿POQ的两直角边分别交于点E、F. 连接EF,探究:在旋转三角形纸板的过程中,△EOF的周长是否存在最小值,若存在,求出最小值,若不存在。请说明理由。
探究画图;19.6;4+2
【解析】
试题分析:(1)

(2) 设AB=AC=xcm,则BC=(x+2)cm,由题意得 解得x=10cm.因此AB=AC=10cm,则BC=12cm,过点A作AD⊥BC于D,∴BD=CD=6cm,∴AD=8cm.
解得x=10cm.因此AB=AC=10cm,则BC=12cm,过点A作AD⊥BC于D,∴BD=CD=6cm,∴AD=8cm.
可以拼成四种四边形,如上图所示.
如图⑴,两对角线之和为10+10=20cm;
如图⑵,AD= ,∴两对角线和为
,∴两对角线和为 ;
;
如图⑶,BC= ,∴两对角线和为
,∴两对角线和为 ;
;
如图⑷,∵ ,∴CO=4.8cm,CD=9.6cm.∴两对角线之和为19.6cm.8分
,∴CO=4.8cm,CD=9.6cm.∴两对角线之和为19.6cm.8分
(3)答:△EOF的周长存在最小值理由是:连接OM
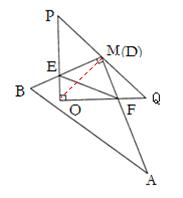
∵ Rt⊿POQ中,OP="OQ" =4,M是PQ的中点
∴OM=PM= PQ=2
PQ=2
∠POM=∠FOM=∠P=45° ∵∠PME+∠EMO=∠OMF+∠EMO
∴∠PME=∠OMF ⊿PME≌⊿OMF
∴ ME=MF
∴ PE=OF ∴OE+OF=OE+PE=OP=4
令OE=x EF=y则y2=x2+(4-x)2=2x2-8x+16
=2(x-2)2+8≥8
当x=2时y2有最小值=8从而 y≥2
故△EOF的周长存在最小值,其最小值是4+2
考点:全等三角形的性质和判定
点评:解答本题的关键是熟练掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
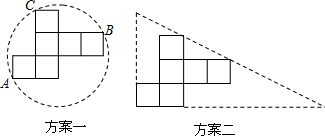
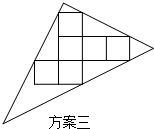
| 纸片被利用的面积 | 纸片的总面积 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 15 |
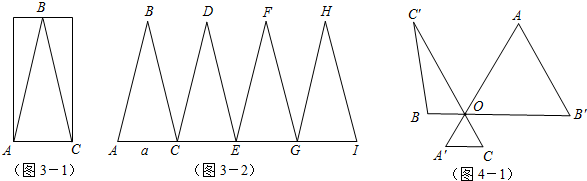
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
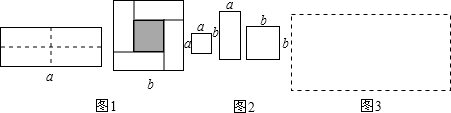
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com