
 矩形ABCD中,E是CD上一点,且AE=CE,F是AC上一点FH⊥AE于H,FG⊥CD于G,求证:FH+FG=AD.
矩形ABCD中,E是CD上一点,且AE=CE,F是AC上一点FH⊥AE于H,FG⊥CD于G,求证:FH+FG=AD. 分析 连接EF,由△ACE的面积=△AEF的面积+△CEF的面积=$\frac{1}{2}$AE•FH+$\frac{1}{2}$CE•FG,△ACE的面积=$\frac{1}{2}$CE•AD,再由AE=CE,即可得出结论.
解答 证明:连接EF,如图所示: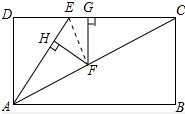
∵FH⊥AE于H,FG⊥CD于G,
∴△ACE的面积=△AEF的面积+△CEF的面积=$\frac{1}{2}$AE•FH+$\frac{1}{2}$CE•FG,
∵AE=CE,
∴△ACE的面积=$\frac{1}{2}$CE(FH+FG),
又∵四边形ABCD是矩形,
∴AD⊥CD,
∴△ACE的面积=$\frac{1}{2}$CE•AD,
∴FH+FG=AD.
点评 本题考查了矩形的性质、三角形面积的计算方法;熟练掌握矩形的性质和三角形面积的计算,作出辅助线是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 某校科技小组进行野外考察,为了安全地通过一片湿地,他们沿着前进路线铺了若干块木块,构筑出一条临时道路.木块对地面的压强p(Pa)是关于木板面积S(m2)的反比例函数,其图象如图所示.
某校科技小组进行野外考察,为了安全地通过一片湿地,他们沿着前进路线铺了若干块木块,构筑出一条临时道路.木块对地面的压强p(Pa)是关于木板面积S(m2)的反比例函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 有许多代数恒等式可以用图形的面积来表示,如图①,它表示(2m+2n)(m+n)=2m2+3mn+n2.观察图②,请你写出三个代数式(m+n)2、(m-n)2、mn之间的等量关系是(m+n)2-4mn=(m-n)2;(m+n)2-(m-n)2=4mn;(m-n)2+4mn=(m+n)2.
有许多代数恒等式可以用图形的面积来表示,如图①,它表示(2m+2n)(m+n)=2m2+3mn+n2.观察图②,请你写出三个代数式(m+n)2、(m-n)2、mn之间的等量关系是(m+n)2-4mn=(m-n)2;(m+n)2-(m-n)2=4mn;(m-n)2+4mn=(m+n)2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com