

���� ��1����AD��BC����ΪD���ӳ�BC��P��ʹ��PA=AP�䣬����AD=APsin30��=��PB+BD��tan30���Լ�PB+PC=PC+CP��=PP��=2��PB+BD��������⣮
��2��AD��BC����ΪD�����߶�CB��ȡһ��P��ʹ��AP=AP�䣬����AD=APsin45��=��BD-PB��tan45�㣬�Լ�PC-PB=2��BD-PB��������⣮
��3����֤����APB�ס�CAF�õ���F=��B�ɡ�AEF=��EDB=90���֪��FEA�ס�BDE��$\frac{EF}{BD}=\frac{EA}{DE}$�����ɽ����
��� ��1��֤���� ��AD��BC����ΪD���ӳ�BC��P��ʹ��PA=AP�䣬
��AD��BC����ΪD���ӳ�BC��P��ʹ��PA=AP�䣬
��AB=AC��AP=AP�䣬
��BD=DC��PD=DP�䣬
��PB=P��C
��PB+PC=PC+CP��=PP��=2��PB+BD��
�ߡ�P=��P��=30�㣬
��AD=APsin30��=��PB+BD��tan30�㣬
��AP$•\frac{1}{2}$=$\frac{1}{2}$��PB+PC��•$\frac{\sqrt{3}}{3}$��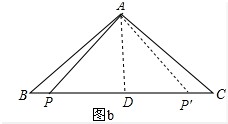
��PB+PC=$\sqrt{3}$AP��
��2�����ۣ�PC-PB=$\sqrt{2}$PA��
֤������ͼb�У���AD��BC����ΪD�����߶�CB��ȡһ��P��ʹ��AP=AP�䣬
��AB=AC��
��BD=DC��DP=DP�䣬BP=P��C��
��AD=APsin45��=��BD-PB��tan45�㣬
��PC-PB=2��BD-PB����
��PC-PB=$\sqrt{2}$PA��
�ʴ�ΪPC-PB=$\sqrt{2}$PA��
��3����ͼ��2��֪��PB=CP��=1��PC=7��EP=EC=$\frac{7\sqrt{2}}{2}$��
��AE=PE-AP��
��AE=$\frac{7\sqrt{2}}{2}$-3$\sqrt{2}$=$\frac{\sqrt{2}}{2}$��AD=PD=DC=3.5��BD=4.5��
�ߡ�BAP=��APC-��B=45��-��B����FCA=��ECP-��ACB=45��-��ACB��
�ߡ�B=��ACB��
���PAB=��FCA��
�ߡ�APB=��FAC=135�㣬
���APB�ס�CAF��
���F=��B��
�ߡ�AEF=��EDB=90�㣬
���FEA�ס�BDE��
��$\frac{EF}{BD}=\frac{EA}{DE}$��
��$\frac{EF}{4.5}=\frac{\frac{\sqrt{2}}{2}}{3.5}$��
��EF=$\frac{9\sqrt{2}}{14}$��
���� ���⿼��������������ʡ����Ǻ��������������ε��ж������ʣ��ۺ��ԱȽ�ǿ�����ݶԳ����������DZ���õ�����Ĺؼ���


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
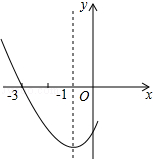 ��ͼ���������ϵ�������y=ax2+bx+c�ĶԳ���Ϊֱ��x=-1���ҹ��㣨-3��0��������˵������abc��0����b-2a=0����4a+2b+c��0��������$\frac{5}{2}$��y1������-5��y2���������������㣬��y1��y2��������ȷ�ĸ����ǣ�������
��ͼ���������ϵ�������y=ax2+bx+c�ĶԳ���Ϊֱ��x=-1���ҹ��㣨-3��0��������˵������abc��0����b-2a=0����4a+2b+c��0��������$\frac{5}{2}$��y1������-5��y2���������������㣬��y1��y2��������ȷ�ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬A��0��6����B��$2\sqrt{3}$��0�����ҡ�OBA=60�㣬����OAB��ֱ��AB���ۣ��õ���CAB����O���C��Ӧ��
��ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬A��0��6����B��$2\sqrt{3}$��0�����ҡ�OBA=60�㣬����OAB��ֱ��AB���ۣ��õ���CAB����O���C��Ӧ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ǵı�Խ������Խ�� | |
| B�� | ����֮����߶Σ��������ľ��� | |
| C�� | ��A��B��P��ͬһֱ���ϣ���AB=2AP����P��AB���е� | |
| D�� | �ڡ�AOB����һ������OC������AOC=��BOC��������OCƽ�֡�AOB |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com