
阅读下面材料:
小明观察一个由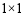 正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1.他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出它们相交所成锐角的正切值.
正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1.他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出它们相交所成锐角的正切值.
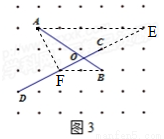
请回答:(1)如图1,A、B、C是点阵中的三个点,请在点阵中找到点D,作出线段CD,使得CD⊥AB;
(2)如图2,线段AB与CD交于点O.为了求出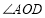 的正切值,小明在点阵中找到了点E,连接AE,恰好满足
的正切值,小明在点阵中找到了点E,连接AE,恰好满足 于F,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
于F,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
请你帮小明计算:OC=_______________;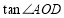 =_______________;
=_______________;
(1)作图见试题解析;(2)OC=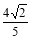 ,
,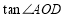 =5;(3)
=5;(3)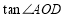 =
=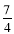 .
.
【解析】
试题分析:(1)用三角板过C作AB的垂线,从而找到D的位置;
(2)连结AC、DB、AD、DE.由△ACO∽△DBO求得CO的长,由等腰直角三角形的性质可以求出AF,DF的长,从而求出OF的长,在Rt△AFO中,根据锐角三角函数的定义即可求出tan∠AOD的值;
(3)如图,连结AE、BF,则AF=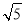 ,AB=
,AB=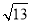 ,由△AOE∽△BOF,可以求出AO=
,由△AOE∽△BOF,可以求出AO= ,在Rt△AOF中,可以求出OF=
,在Rt△AOF中,可以求出OF= ,故可以求得
,故可以求得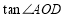 .
.
试题解析:(1)如图,线段CD即为所求;
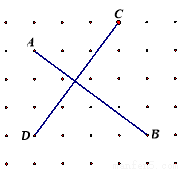
(2)连结AC、DB、AD、DE.∵AD=DE=2,∴AE=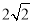 ,∵CD⊥AE,∴DF=AF=
,∵CD⊥AE,∴DF=AF=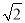 ,∵AC∥DB,∴△ACO∽△DBO,∴CO:DO=2:3,∴CO=
,∵AC∥DB,∴△ACO∽△DBO,∴CO:DO=2:3,∴CO=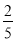 CD=
CD=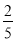
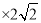 =
=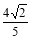 ,∴DO=
,∴DO=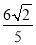 ,∴OF=
,∴OF=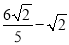 =
=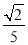 ,∴
,∴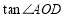 =
=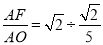 =5;
=5;
(3)如图,连结AE、BF,则AF=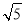 ,AB=
,AB=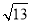 ,BF=2,AE=5,∵FB∥AE,∴△AOE∽△BOF,∴AO:OB=AE:FB=5:2,∴AO=
,BF=2,AE=5,∵FB∥AE,∴△AOE∽△BOF,∴AO:OB=AE:FB=5:2,∴AO=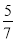 AB=
AB= ,在Rt△AOF中,OF=
,在Rt△AOF中,OF=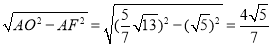 ,∴
,∴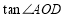 =
=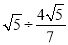 =
=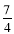 .
.
考点:1.相似三角形的判定与性质;2.锐角三角函数的定义.


科目:初中数学 来源:2014-2015学年北京市通州区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知二次函数 的图象经过A(2,0)B(0,-6)两点.求这个二次函数的表达式.
的图象经过A(2,0)B(0,-6)两点.求这个二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:填空题
一个扇形的圆心角为120°,半径为3,则这个扇形的弧长为 .(结果保留 )
)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市石景山区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,A,B,C都是⊙O上的点,若∠ABC=110°,则∠AOC的度数为( )

A.70° B.110° C.135° D.140°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系 中,正比例函数
中,正比例函数 与反比例函数
与反比例函数 的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.

(1)求反比例函数的解析式;
(2)若点P是反比例函数 图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:填空题
在某一时刻,测得一根高为2m的竹竿的影长为1m,同时测得一栋建筑物的影长为12m,那么这栋建筑物的高度为 m.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,正比例函数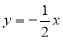 的图象与反比例函数
的图象与反比例函数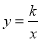 的图象分别交于M,N两点,已知点M(-2,m).
的图象分别交于M,N两点,已知点M(-2,m).

(1)求反比例函数的表达式;
(2)点P为y轴上的一点,当∠MPN为直角时,直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com