
【题目】如图,⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作⊙O的切线交AC的延长线于点E.求DE的长.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明袋子中有1个红球、1 个绿球和n个白球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,记录下颜色后放回袋子中并搅匀.经大量试验,发现摸到白球的频率稳定在0.75左右,求n的值;
(2)当n=2时,把袋中的球搅匀后任意摸出2个球,用树状图或列表求摸出的2个球颜色不同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 有一组邻边相等的四边形是菱形
B. 有一个角是直角的平行四边形是矩形
C. 对角线垂直的平行四边形是正方形
D. 一组对边平行的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.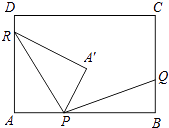
(1)若k=4,PA=15,则四边形PARA′的形状是;
(2)设DR=x,点B关于直线PQ的对称点为B′点.
①记△PRA′的面积为S1 , △PQB′的面积为S2 . 当S1<S2时,求相应x的取值范围及S2﹣S1的最大值;(用含k的代数式表示)
②在点P的运动过程中,判断点B′能否与点A′重合?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=﹣x和反比例函数 ![]() (k>0),点A(m,n)(m>0)在反比例函数
(k>0),点A(m,n)(m>0)在反比例函数![]() 上.
上.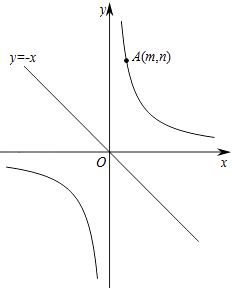
(1)当m=n=2时,
①直接写出k的值;
②将直线y=﹣x作怎样的平移能使平移后的直线与反比例函数 ![]() 只有一个交点.
只有一个交点.
(2)将直线y=﹣x绕着原点O旋转,设旋转后的直线与反比例函数 ![]() 交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:
交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问: ![]() 与
与 ![]() 的值存在怎样的数量关系?请说明理由.
的值存在怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备与汽车租凭公司签订租车合同,以每月用车路程x km计算,甲汽车租凭公司每月收取的租赁费为y1元,乙汽车租凭公司每月收取的租赁费为y2元,若y1、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( ) 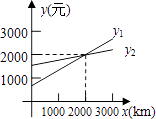
A.当月用车路程为2000km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2300km时,租赁乙汽车租赁公司车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙公司多
D.甲租赁公司每月的固定租赁费高于乙租赁公司
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P为AB的中点,求PG的长.
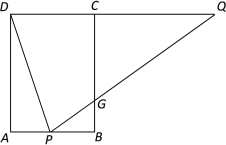
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列算式:①(a3)2=a3×2=a6;②aman=am+n(m,n为正整数);③[(-x)4]5=-x20.其中正确的算式有( ).
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com