
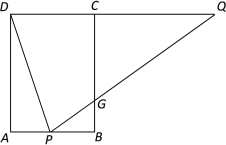
【题目】如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P为AB的中点,求PG的长.
【答案】(1)证明见解析;(2)26;(3)![]()
【解析】试题分析:(1)要证DQ=PQ,即证∠QPD=∠QDP,又因为已知∠APD=∠QPD,即证∠APD=∠QDP,即证AB∥CD,由四边形ABDF是矩形得到AB∥CD;(2)过点Q作QE⊥DP,垂足为E,则DE=![]() DP,先证△QDE∽△DPA,
DP,先证△QDE∽△DPA,
得出![]() =
=![]() , 所以AP·DQ=DP·DE=
, 所以AP·DQ=DP·DE=![]() DP2,在Rt△DAP中,有DP2=DA2+AP2=36+AP2,所以AP·DQ=
DP2,在Rt△DAP中,有DP2=DA2+AP2=36+AP2,所以AP·DQ=![]() (36+AP2),又由点P在AB上,故AP≤4,所以AP·DQ≤26,即AP·DQ的最大值为26;(3)由P为AB的中点得到AP=BP=
(36+AP2),又由点P在AB上,故AP≤4,所以AP·DQ≤26,即AP·DQ的最大值为26;(3)由P为AB的中点得到AP=BP=![]() AB=2,由(2)得,DQ=
AB=2,由(2)得,DQ=![]() (36+22)=10,所以CQ=DQ-DC=6.设CG=x,则BG=6-x,由(1)得,DQ∥AB,所以
(36+22)=10,所以CQ=DQ-DC=6.设CG=x,则BG=6-x,由(1)得,DQ∥AB,所以![]() =
=![]() ,即
,即![]() =
=![]() ,解得x=
,解得x=![]() ,所以BG=6-
,所以BG=6-![]() =
=![]() ,所以PG=
,所以PG=![]() =
=![]() .
.
试题解析:
(1)∵四边形ABDF是矩形,
∴AB∥CD,
∴∠APD=∠QDP.
∵∠APD=∠QPD,
∴∠QPD=∠QDP,
∴DQ=PQ.
(2)过点Q作QE⊥DP,垂足为E,则DE=![]() DP,如图所示:
DP,如图所示:
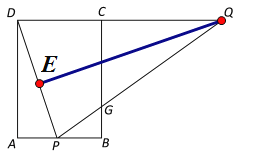
∵∠DEQ=∠PAD=90°,∠QDP=∠APD,
∴△QDE∽△DPA,
∴![]() =
=![]() ,
,
∴AP·DQ=DP·DE=![]() DP2.
DP2.
在Rt△DAP中,有DP2=DA2+AP2=36+AP2,
∴AP·DQ=![]() (36+AP2).
(36+AP2).
∵点P在AB上,
∴AP≤4,
∴AP·DQ≤26,即AP·DQ的最大值为26.
(3)∵P为AB的中点,
∴AP=BP=![]() AB=2,
AB=2,
由(2)得,DQ=![]() (36+22)=10.
(36+22)=10.
∴CQ=DQ-DC=6.设CG=x,则BG=6-x,
由(1)得,DQ∥AB,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,解得x=
,解得x=![]() ,
,
∴BG=6-![]() =
=![]() ,
,
∴PG=![]() =
=![]() .
.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,属于真命题的是( )
A.对角线互相垂直的四边形是平行四边形B.对角线互相垂直平行的四边形是菱形
C.对角线互相垂直且相等的四边形是矩形D.对角线互相平分且相等的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF. 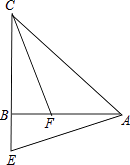
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
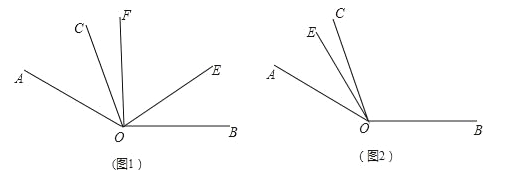
【题目】如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=30°,则∠COF= ;
(2)若∠COF=20°,则∠EOB= ;
(3)若∠COF=n°,则∠EOB= (用含n的式子表示).
(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈2.4)
≈2.4)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com