
【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF. 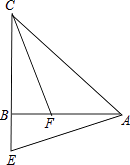
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
【答案】
(1)证明:在Rt△ABE和Rt△CBF中,
∵ ![]() ,
,
∴Rt△ABE≌Rt△CBF(HL)
(2)如图,∵在△ABC中,AB=CB,∠ABC=90°,
∴∠ACB=∠CAB=45°,
∴∠BAE=∠CAE﹣∠CAB=15°.
又由(1)知,Rt△ABE≌Rt△CBF,
∴∠BAE=∠BCF=15°,
∴∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度数是30°
【解析】(1)在Rt△ABE和Rt△CBF中,由于AB=CB,AE=CF,利用HL可证Rt△ABE≌Rt△CBF;(2)由等腰直角三角形的性质易求∠BAE=∠CAE﹣∠CAB=15°.利用(1)中全等三角形的对应角相等得到∠BAE=∠BCF=15°,则∠ACF=∠ACB﹣∠BCF=30°.即∠ACF的度数是30°.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
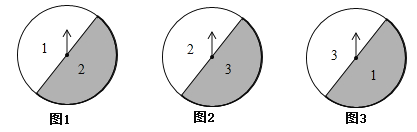
【题目】如图①、②、③是三个可以自由转动的转盘.
(1)若同时转动①、②两个转盘,则两个转盘停下时指针所指的数字都是2的概率为 ;
(2)甲、乙两人用三个转盘玩游戏,甲转动转盘,乙记录指针停下时所指的数字.游戏规定:当指针所指的三个数字中有数字相同时,就算甲赢,否则就算乙赢.请判断这个游戏是否公平,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8k,BC=5k(k为常数,且k>0),动点P在AB边上(点P不与A、B重合),点Q、R分别在BC、DA边上,且AP:BQ:DR=3:2:1.点A关于直线PR的对称点为A′,连接PA′、RA′、PQ.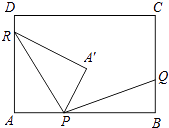
(1)若k=4,PA=15,则四边形PARA′的形状是;
(2)设DR=x,点B关于直线PQ的对称点为B′点.
①记△PRA′的面积为S1 , △PQB′的面积为S2 . 当S1<S2时,求相应x的取值范围及S2﹣S1的最大值;(用含k的代数式表示)
②在点P的运动过程中,判断点B′能否与点A′重合?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备与汽车租凭公司签订租车合同,以每月用车路程x km计算,甲汽车租凭公司每月收取的租赁费为y1元,乙汽车租凭公司每月收取的租赁费为y2元,若y1、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( ) 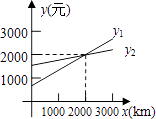
A.当月用车路程为2000km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2300km时,租赁乙汽车租赁公司车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙公司多
D.甲租赁公司每月的固定租赁费高于乙租赁公司
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备与汽车租凭公司签订租车合同,以每月用车路程x km计算,甲汽车租凭公司每月收取的租赁费为y1元,乙汽车租凭公司每月收取的租赁费为y2元,若y1、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( ) 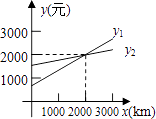
A.当月用车路程为2000km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2300km时,租赁乙汽车租赁公司车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙公司多
D.甲租赁公司每月的固定租赁费高于乙租赁公司
查看答案和解析>>
科目:初中数学 来源: 题型:
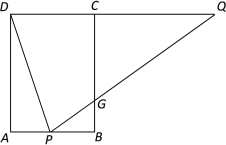
【题目】如图,矩形ABCD中,AB=4,AD=6,点P在AB上,点Q在DC的延长线上,连接DP,QP,且∠APD=∠QPD,PQ交BC于点G.
(1)求证:DQ=PQ;
(2)求AP·DQ的最大值;
(3)若P为AB的中点,求PG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的解是一元一次不等式组的解,那么称该一元一次方程为该不等式组的关联方程.
(1)若不等式组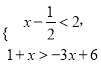 的一个关联方程的解是整数,则这个关联方程可以是 (写出一个即可);
的一个关联方程的解是整数,则这个关联方程可以是 (写出一个即可);
(2)若方程3-x=2x,3+x=2(x+![]() )都是关于
)都是关于![]() 的不等式组
的不等式组![]() 的关联方程,试求
的关联方程,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由. 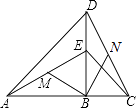
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com