
【题目】如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= 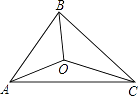
【答案】4:5:6
【解析】解:过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,
∵OA,OB,OC是△ABC的三条角平分线,
∴OD=OE=OF,
∵△ABC的三边AB、BC、CA长分别为40、50、60,
∴S△ABO:S△BCO:S△CAO=( ![]() ABOD):(
ABOD):( ![]() BCOF):(
BCOF):( ![]() ACOE)=AB:BC:AC=40:50:60=4:5:6.
ACOE)=AB:BC:AC=40:50:60=4:5:6.
故答案为:4:5:6.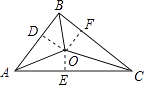
首先过点O作OD⊥AB于点D,作OE⊥AC于点E,作OF⊥BC于点F,由OA,OB,OC是△ABC的三条角平分线,根据角平分线的性质,可得OD=OE=OF,又由△ABC的三边AB、BC、CA长分别为40、50、60,即可求得S△ABO:S△BCO:S△CAO的值.


科目:初中数学 来源: 题型:
【题目】一次知识竞赛共有20道选择题,规定:答对一道得5分,不答或答错一道扣1分,如果某位学生答对了x道题,则用式子表示他的成绩为( )
A. 5x﹣(20+x)B. 100﹣(20﹣x)C. 5xD. 5x﹣(20﹣x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF. 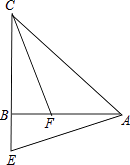
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=30°,则∠COF= ;
(2)若∠COF=20°,则∠EOB= ;
(3)若∠COF=n°,则∠EOB= (用含n的式子表示).
(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
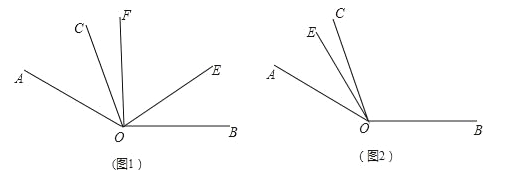
查看答案和解析>>
科目:初中数学 来源: 题型:
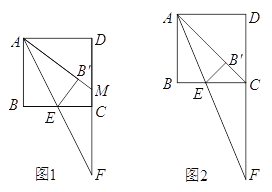
【题目】如图,正方形ABCD的边长为12,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B'处.
(1)当![]() =1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
=1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
(2)当点B'恰好落在对角线AC上时,如图2,此时CF的长为 ; ![]() = .
= .
(3)当![]() =3时,求∠DA B'的正弦值.
=3时,求∠DA B'的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一棵大树AB(假定大树AB垂直于地面)被刮倾斜15°后折断在地上,树的顶部恰好接触到地面D处(如示意图所示),量得大树的倾斜角∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求大树AB原来的高度是多少米?(结果保留整数,参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,
≈1.7, ![]() ≈2.4)
≈2.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x(x+1)=x+1的解是( )
A. x1=0,x2=-1 B. x = 1 C. x1 = x2 = 1 D. x1 = 1,x2=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com