
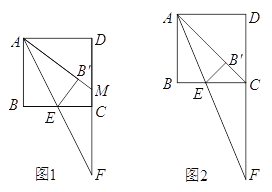
【题目】如图,正方形ABCD的边长为12,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B'处.
(1)当![]() =1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
=1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
(2)当点B'恰好落在对角线AC上时,如图2,此时CF的长为 ; ![]() = .
= .
(3)当![]() =3时,求∠DA B'的正弦值.
=3时,求∠DA B'的正弦值.
【答案】(1)①CF的长为12;②证明见解析;
2)CF的长为12![]() ,
, ![]() =
=![]() ;
;
(3)当![]() 时,∠DA B'的正弦值为
时,∠DA B'的正弦值为![]() 或
或![]() .
.
【解析】解:(1)①CF的长为 12 ;
②证明:∵四边形ABCD为正方形,
∴AB∥CD,∴∠ F=∠ BAF,
由折叠可知:∠ BAF=∠ MAF,
∴∠ F=∠ MAF,∴AM=FM.
(2)CF的长为12![]() ;
;
![]() =
=![]() .
.
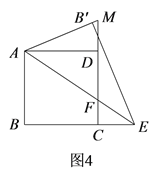
(3)①当点E在线段BC上时,如图3,
 A B'的延长线交CD于点M,易证:△ABE∽△FCE,
A B'的延长线交CD于点M,易证:△ABE∽△FCE,
∴![]() ,即
,即![]() ,∴CF=4,
,∴CF=4,
由(1)②证明可知:
AM=FM.设DM=x,则MC=12-x,则AM=FM=16-x,
在Rt△ADM中, ![]() ,
,
 即(16-x)2=122+x2,解得:x=
即(16-x)2=122+x2,解得:x=![]() ,
,
则16-x=16-![]() =
=![]() ,
,
∴sin∠DA B'=![]() =
=![]() .
.
②当点E在BC的延长线上时,如图4,
易证:△ABE∽△FCE,
∴![]() ,即
,即![]() ,∴CF=4,
,∴CF=4,
则DF=12-4=8,设DM=x,则AM=FM=8+x,
在Rt△ADM中, ![]() ,
,
即(8+x)2=122+x2,解得:x=5,则AM=8+x=13,
∴sin∠DA B'=![]() =
=![]() .
.
综上所述:当![]() 时,∠DA B'的正弦值为
时,∠DA B'的正弦值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司准备与汽车租凭公司签订租车合同,以每月用车路程x km计算,甲汽车租凭公司每月收取的租赁费为y1元,乙汽车租凭公司每月收取的租赁费为y2元,若y1、y2与x之间的函数关系如图所示(其中x=0对应的函数值为月固定租赁费),则下列判断错误的是( ) 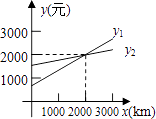
A.当月用车路程为2000km时,两家汽车租赁公司租赁费用相同
B.当月用车路程为2300km时,租赁乙汽车租赁公司车比较合算
C.除去月固定租赁费,甲租赁公司每公里收取的费用比乙公司多
D.甲租赁公司每月的固定租赁费高于乙租赁公司
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的解是一元一次不等式组的解,那么称该一元一次方程为该不等式组的关联方程.
(1)若不等式组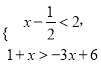 的一个关联方程的解是整数,则这个关联方程可以是 (写出一个即可);
的一个关联方程的解是整数,则这个关联方程可以是 (写出一个即可);
(2)若方程3-x=2x,3+x=2(x+![]() )都是关于
)都是关于![]() 的不等式组
的不等式组![]() 的关联方程,试求
的关联方程,试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,其部分图象如图所示,给出下列四个结论:①
,其部分图象如图所示,给出下列四个结论:①![]() ; ②
; ②![]() ;③
;③![]() ;④若点
;④若点![]() 在抛物线上,则
在抛物线上,则![]() .其中结论正确的是( )
.其中结论正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com