
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 先根据此三角形是直角三角形利用勾股定理把原式化为(a-6)(b-6)=18,再根据a,b均为正整数,不妨设a<b,可得出关于a、b的二元一次方程,求出a、b、c的对应值即可.
解答 解:由勾股定理得c2=a2+b2.
又∵c=$\frac{1}{3}$ab-(a+b),
∴c2=[$\frac{1}{3}$ab-(a+b)]2=$\frac{1}{9}$(ab)2-$\frac{2}{3}$ab(a+b)+(a+b)2,即a2+b2=$\frac{1}{9}$(ab)2-$\frac{2}{3}$ab(a+b)+a2+b2+2ab,
整理得,ab-6(a+b)+18=0,即(a-6)(b-6)=18,
∵a,b均为正整数,不妨设a<b,
可得$\left\{\begin{array}{l}a-6=1\\ b-6=18\end{array}\right.$或$\left\{\begin{array}{l}a-6=2\\ b-6=9\end{array}\right.$或$\left\{\begin{array}{l}a-6=3\\ b-6=6\end{array}\right.$,
可解出$\left\{\begin{array}{l}a=7\\ b=2\\ c=25\end{array}\right.$或$\left\{\begin{array}{l}a=8\\ b=15\\ c=17\end{array}\right.$或$\left\{\begin{array}{l}a=9\\ b=12\\ c=15\end{array}\right.$,
∴满足条件的直角三角形有3个.
故选C.
点评 本题考查的是三角形的三边关系,涉及到非一次不定方程及勾股定理,解答此题的关键是先利用勾股定理把原式化为两个因式积的形式,再根据a,b均为正整数进行解答.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
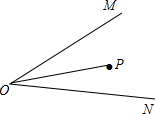 如图,已知∠MON=30°,点P为∠MON内一点,且OP=8,点A为OM上一点,点B为ON上一点.
如图,已知∠MON=30°,点P为∠MON内一点,且OP=8,点A为OM上一点,点B为ON上一点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 零减去任何一个数都是负数 | |
| B. | 任何两个数的和都不等于这两个数的差 | |
| C. | 减去一个负数等于加上一个正数 | |
| D. | 两个数的差不一定小于它们的和 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com