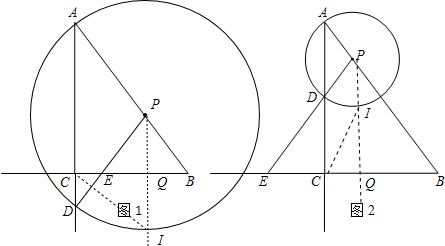
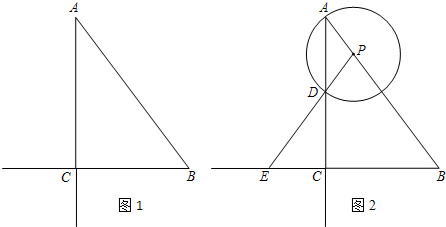
解:(1)①如图2∵AP=DP,
∴∠PAD=∠PDA,
∵∠PDA=∠CDE,
∴∠PAD=∠CDE,
∵∠ACB=∠DCE=90°,
∴△ABC∽△DEC,
∴∠ABC=∠DEC,
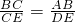
.
∴PB=PE.
在Rt△ABC中,∠ABC=90°,AC=4,BC=3,
∴AB=

=5,
∴PB=PE=5-x,DE=PE-PD=5-x-x=5-2x,
∴
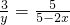
,
∴y=-

x+3(0<x<

);
②设BE的中点为Q,连结PQ,如图2,
∵PB=PE,
∴PQ⊥BE,
又∵∠ACB=90°,
∴PQ∥AC,
∴△BPQ∽△BAC,
∴
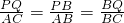
,即
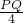
=

=
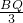
,
∴PQ=-

x+4,BQ=-

x+3,
当以BE为直径的圆和⊙P外切时,-

x+4=x+(-

x+3),解得x=

,即AP的长为

;
(2)当点E在线段BC延长线上时,
由(1)②的结论可得IQ=PQ-PI=-

x+4-x=-

x+4,
CQ=BC-BQ=3-(-

x+3)=

x,
在Rt△CQI中,CI
2=CQ
2+IQ
2=(

x)
2+(-

x+4)
2=

x
2-

x+16,
∵CI=AP,
∴

x
2-

x+16=x
2,
解得x
1=

,x
2=4(不合题意,舍去),
∴AP的长为

;
当点E在线段BC上时,IQ=PI-PQ=x-(-

x+4)=

x-4,
CQ=BC-BQ=3-(-

x+3)=

x,
在Rt△CQI中,CI
2=CQ
2+IQ
2=(

x)
2+(

x-4)
2=

x
2-

x+16,
∵CI=AP,
∴

x
2-

x+16=x
2,
解得x
1=

(舍去),x
2=4,
∴AP的长为4,
综上所述,AP的长为

或4.
分析:(1)①由AP=DP得到∠PAD=∠PDA,由对顶角相等得∠PDA=∠CDE,则∠PAD=∠CDE,根据三角形相似的判定方法得到△ABC∽△DEC,则∠ABC=∠DEC,
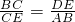
,且得到PB=PE.在Rt△ABC中根据勾股定理计算出AB=5,则PB=PE=5-x,DE=5-2x,然后利用相似比即可得到y关于x的函数关系式;
②设BE的中点为Q,连结PQ,由于PB=PE,根据等腰三角形的性质得PQ⊥BE,易得PQ∥AC,则△BPQ∽△BAC,利用相似比得到PQ=-

x+4(圆心距),BQ=-

x+3(⊙Q的半径),根据两圆外切的性质得到-

x+4=x+(-

x+3),然后解方程即可;
(2)分类讨论:当点E在线段BC延长线上时,利用(1)②的结论可得IQ=PQ-PI=-

x+4,CQ=BC-BQ=

x,在Rt△CQI中,根据勾股定理得CI
2=CQ
2+IQ
2=(

x)
2+(-

x+4)
2=

x
2-

x+16,再由CI=AP得到

x
2-

x+16=x
2,解得x
1=

,x
2=4,由于0<x<

,由此得到AP的长为

;
同理当点E在线段BC上时,IQ=PI-PQ=

x-4,CQ=BC-BQ=

x,在Rt△CQI中,CI
2=CQ
2+IQ
2=

x
2-

x+16,利用CI=AP得到

x
2-

x+16=x
2,解得x
1=

,x
2=4,由于

<x<5,则AP的长为4,由此得到AP的长为

或4.
点评:本题考查了圆的综合题:熟练掌握两圆相切的性质和三角形相似的判定与性质;会运用勾股定理和相似比进行几何计算;能运用分类讨论的思想解决问题.

 解:(1)①如图2∵AP=DP,
解:(1)①如图2∵AP=DP,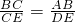 .
. =5,
=5,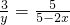 ,
, x+3(0<x<
x+3(0<x< );
);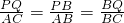 ,即
,即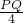 =
= =
=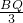 ,
, x+4,BQ=-
x+4,BQ=- x+3,
x+3, x+4=x+(-
x+4=x+(- x+3),解得x=
x+3),解得x= ,即AP的长为
,即AP的长为 ;
; x+4-x=-
x+4-x=- x+4,
x+4, x+3)=
x+3)= x,
x, x)2+(-
x)2+(- x+4)2=
x+4)2= x2-
x2- x+16,
x+16, x2-
x2- x+16=x2,
x+16=x2, ,x2=4(不合题意,舍去),
,x2=4(不合题意,舍去), ;
; x+4)=
x+4)= x-4,
x-4, x+3)=
x+3)= x,
x, x)2+(
x)2+( x-4)2=
x-4)2= x2-
x2- x+16,
x+16, x2-
x2- x+16=x2,
x+16=x2, (舍去),x2=4,
(舍去),x2=4, 或4.
或4.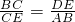 ,且得到PB=PE.在Rt△ABC中根据勾股定理计算出AB=5,则PB=PE=5-x,DE=5-2x,然后利用相似比即可得到y关于x的函数关系式;
,且得到PB=PE.在Rt△ABC中根据勾股定理计算出AB=5,则PB=PE=5-x,DE=5-2x,然后利用相似比即可得到y关于x的函数关系式; x+4(圆心距),BQ=-
x+4(圆心距),BQ=- x+3(⊙Q的半径),根据两圆外切的性质得到-
x+3(⊙Q的半径),根据两圆外切的性质得到- x+4=x+(-
x+4=x+(- x+3),然后解方程即可;
x+3),然后解方程即可; x+4,CQ=BC-BQ=
x+4,CQ=BC-BQ= x,在Rt△CQI中,根据勾股定理得CI2=CQ2+IQ2=(
x,在Rt△CQI中,根据勾股定理得CI2=CQ2+IQ2=( x)2+(-
x)2+(- x+4)2=
x+4)2= x2-
x2- x+16,再由CI=AP得到
x+16,再由CI=AP得到 x2-
x2- x+16=x2,解得x1=
x+16=x2,解得x1= ,x2=4,由于0<x<
,x2=4,由于0<x< ,由此得到AP的长为
,由此得到AP的长为 ;
; x-4,CQ=BC-BQ=
x-4,CQ=BC-BQ= x,在Rt△CQI中,CI2=CQ2+IQ2=
x,在Rt△CQI中,CI2=CQ2+IQ2= x2-
x2- x+16,利用CI=AP得到
x+16,利用CI=AP得到 x2-
x2- x+16=x2,解得x1=
x+16=x2,解得x1= ,x2=4,由于
,x2=4,由于 <x<5,则AP的长为4,由此得到AP的长为
<x<5,则AP的长为4,由此得到AP的长为 或4.
或4.

 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论: (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 的外接圆.
的外接圆. (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.