
【题目】如图,在正方形网格中,△TAB顶点坐标分别为T(1,1)、A(2,3)、B(4,2).

(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.
【答案】(1)
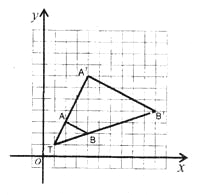
A′(4,7),B′(10,4)
(2)C′(3a-2,3b-2)
【解析】试题分析:(1)依题意知,以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1的位似中心的同侧将TAB放大为△TA′B′,故TA’=3TA,B’T=3BT。则延长如图,连结A’B’得△TA′B′。
由图可得A′坐标为(4,7),B′坐标为(10,4);
(2) 易知A、B坐标由A(2,3),B(4,2)变化为A′(4,7),B′(10,4);
则x值变化=3x-2,y值变化=3y-2;
若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标,则变化后点C的对应点C′的坐标为:C′(3a-2,3b-2)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣m)2+n与y轴交于点A,它的顶点为点B,点A、B关于原点O的对称点分别为C、D.若A、B、C、D中任何三点都不在一直线上,则称四边形ABCD为抛物线的伴随四边形,直线AB为抛物线的伴随直线.
(1)如图1,求抛物线y=(x﹣2)2+1的伴随直线的解析式.
(2)如图2,若抛物线y=a(x﹣m)2+n(m>0)的伴随直线是y=x﹣3,伴随四边形的面积为12,求此抛物线的解析式.
(3)如图3,若抛物线y=a(x﹣m)2+n的伴随直线是y=﹣2x+b(b>0),且伴随四边形ABCD是矩形.

①用含b的代数式表示m、n的值;
②在抛物线的对称轴上是否存在点P,使得△PBD是一个等腰三角形?若存在,请直接写出点P的坐标(用含b的代数式表示);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若点P在第四象限,且到X轴的距离是2,到Y轴的距离是4,则P点的坐标为( )
A. (2,4)B. (-4,2)C. (4,-2)D. (-2,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某酒家为了了解市民对去年销量较好的五仁馅、豆沙馅、红枣馅、双黄馅四种不同口味月饼(以下分别用A,B,C,D表示)的喜爱情况,在节前对人口总数8000人的某社区市民进行了抽样情况调查,绘制成如图的两幅统计图(尚不完整),请根据信息回答:

(1)将两幅不完整的图补充完整,并估计该社区爱吃D型月饼的人数;
(2)若有外型完全相同的A,B,C,D月饼各一个,小王吃了两个,求她第二个吃到的月饼恰好是C型的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为( )
A. 4.995×1011 B. 49.95×1010 C. 0.4995×1011 D. 4.995×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
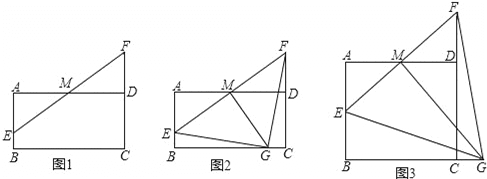
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连结EM并延长交线段CD的延长线于点F.
(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作MG⊥EF交线段BC于点G,求证:△GEF是等腰直角三角形;
(3)如图3,若AB=2![]() ,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
,过点M作MG⊥EF交线段BC的延长线于点G.求线段AE长度的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com