
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
解:(1)y=(x﹣50)[50+5(100﹣x)]
=(x﹣50)(﹣5x+550)
=﹣5x2+800x﹣27500
∴y=﹣5x2+800x﹣27500(50≤x≤100);
(2)y=﹣5x2+800x﹣27500
=﹣5(x﹣80)2+4500
∵a=﹣5<0,
∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500;
(3)当y=4000时,﹣5(x﹣80)2+4500=4000,
解得x1=70,x2=90.
∴当70≤x≤90时,每天的销售利润不低于4000元.
由每天的总成本不超过7000元,得50(﹣5x+550)≤7000,
解得x≥82.
∴82≤x≤90,
∵50≤x≤100,
∴销售单价应该控制在82元至90元之间.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
空气质量状况已引起全社会的广泛关注,某市统计了2013年每月空气质量达到良好以上的天数,整理后制成如下折线统计图和扇形统计图.

根据以上信息解答下列问题:
(1)该市2013年每月空气质量达到良好以上天数的中位数是 天,众数是 天;
(2)求扇形统计图中扇形A的圆心角的度数;
(3)根据以上统计图提供的信息,请你简要分析该市的空气质量状况(字数不超过30字).
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知点A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一根长为2014个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是 .
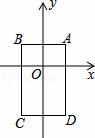
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.
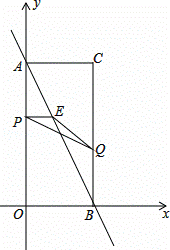
查看答案和解析>>
科目:初中数学 来源: 题型:
对于平面直角坐标系中任意两点P1(x1,y1)、P2(x2,y2),称|x1﹣x2|+|y1﹣y2|为P1、P2两点的直角距离,记作:d(P1,P2).若P0(x0,y0)是一定点,Q(x,y)是直线y=kx+b上的一动点,称d(P0,Q)的最小值为P0到直线y=kx+b的直角距离.令P0(2,﹣3).O为坐标原点.则:
(1)d(O,P0)= ;
(2)若P(a,﹣3)到直线y=x+1的直角距离为6,则a= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com