
��ͼ����ƽ��ֱ������ϵ�У���֪����AOBC�Ķ���C�������ǣ�2��4��������P�ӵ�A���������߶�AO���յ�O�˶���ͬʱ����Q�ӵ�B���������߶�BC���յ�C�˶�����P��Q���˶��ٶȾ�Ϊ1����λ���˶�ʱ��Ϊt�룮����P��PE��AO��AB�ڵ�E��
��1����ֱ��AB�Ľ���ʽ��
��2�����PEQ�����ΪS����S��tʱ��ĺ�����ϵ����ָ���Ա���t��ȡֵ��Χ��
��3���ڶ���P��Q�˶��Ĺ����У���H�Ǿ���AOBC�ڣ������߽磩һ�㣬����B��Q��E��HΪ������ı��������Σ�ֱ��д��tֵ�������Ӧ�ĵ�H�����꣮
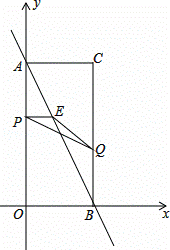
�⣺��1����C��2��4����
��A��0��4����B��2��0����
��ֱ��AB�Ľ���ʽΪy=kx+b��
��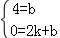 ��
��
���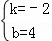
��ֱ��AB�Ľ���ʽΪy=﹣2x+4��
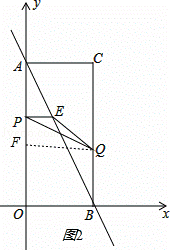
��2����ͼ2������Q��QF��y����F��
��PE��OB��
��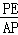 =
=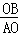 =
=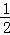
����AP=BQ=t��PE=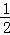 t��AF=CQ=4﹣t��
t��AF=CQ=4﹣t��
��0��t��2ʱ��PF=4﹣2t��
��S= PE•PF=
PE•PF= ��
�� t��4﹣2t��=t﹣
t��4﹣2t��=t﹣ t2��
t2��
��S=﹣ t2+t��0��t��2����
t2+t��0��t��2����
��2��t��4ʱ��PF=2t﹣4��
��S= PE•PF=
PE•PF= ��
�� t��2t﹣4��=
t��2t﹣4��= t2﹣t��2��t��4����
t2﹣t��2��t��4����
��3��t1=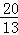 ��H1 ��
��H1 ��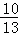 ��
��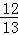 ����
����
t2=20﹣8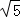 ��H2��10﹣4
��H2��10﹣4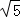 ��4����
��4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ�ֱ���ij��ȫ��ѧ����ѧʱ�˳������С��ﳵ�����ķֲ�ֱ��ͼ������ͳ��ͼ����ͼ���������������н��۴�����ǣ�������

| �� | A�� | �ð�������Ϊ50�� | B�� | ��������Ϊ30�� |
| �� | C�� | �˳��������ﳵ������2.5�� | D�� | �ﳵ����ռ20% |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺������ۣ�Ͷ���г��������������г����飬���۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ���
��1�����ÿ�����������y��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2��������۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3���������ҵҪʹÿ�������������4000Ԫ����ÿ����ܳɱ�������7000Ԫ����ô���۵���Ӧ������ʲô��Χ�ڣ���ÿ����ܳɱ�=ÿ���ijɱ���ÿ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��һ���ɶ����ͬС�������ɵļ�����ĸ���ͼ��ͼ����������Ϊ��λ��С������ĸ���������������������ͼ�ǣ�������

| �� | A�� |
| B�� |
| C�� |
| D�� |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
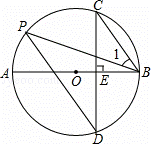
��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�E����P�ڡ�O�ϣ���1=��BCD��
��1����֤��CB��PD��
��2����BC=3��sin��BPD=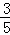 �����O��ֱ����
�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
������̰������ѧ�̲���ʹ�õ�ij�ּ��������м��㣬���Ľ��Ϊ��������

| �� | A�� | 21 | B�� | 15 | C�� | 84 | D�� | 67 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
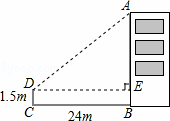
��ͼ��Ϊ����ij������ĸ߶�AB������ý�����ײ�24�ĵ�C����Ŀ�⽨���ﶥ��A����������ˮƽ�нǡ�ADEΪ39�㣬�Ҹ�CDΪ1.5�ף�������ĸ߶�AB���������ȷ��0.1�ף����ο����ݣ�sin39��=0.63��cos39��=0.78��tan39��=0.81��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com