在平面直角坐标系中，点O为原点，抛物线y=ax2+bx（其中-1≤a＜0）经过A（3，n），AB⊥y轴于B，抛物线交直线AB于M．
（1）若n=1，AB=3BM，求抛物线所对应的函数关系式；
（2）若n=a+b，抛物线与x轴另一个异于原点的交点为C，过点A作AP∥OM交直线MC于点P，当△OPM的面积最大时，求sin∠MOP的值．
科目：初中数学 来源：2014-2015学年广东省东莞市五校联考中考一模数学试卷（解析版） 题型：选择题
月球离地球平均距离是384 400 000米，数据384 400 000用科学记数法表示为（ ）
A．3．844×108 B．3．844×107 C．3．844×106 D．38．44×106
查看答案和解析>>
科目：初中数学 来源：2014-2015学年福建省厦门市同安区中考适应性数学试卷（解析版） 题型：选择题
如图，AB为⊙O的弦，OA=4，∠AOB=120°，则AB的长为（ ）
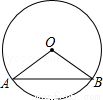
A．4 B．2
C．2 D．4
查看答案和解析>>
科目：初中数学 来源：2014-2015学年福建省厦门市集美区中考适应性数学试卷（解析版） 题型：解答题
一根蜡烛高20cm，蜡烛高度 y（单位：cm）随燃烧的时间x（单位：分钟）的增加而减少，平均每分钟减少量为0．1cm/分钟．求y与x的函数关系式，并画出该函数的图象．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年福建省泉州市晋江市中考适应性数学试卷（解析版） 题型：解答题
一队学生从学校出发去劳动基地军训，行进的路程与时间的图象如图所示，队伍走了0．9小时后，队伍中的通讯员按原路加快速度返回学校拿材料，通讯员经过0．5小时后回到学校，然后随即按原来加快的速度追赶队伍，恰好在劳动基地追上学生队伍．设学生队伍与学校的距离为d1，通讯员与学校的距离为d2，试根据图象解决下列问题：
（1）填空：学生队伍的行进速度v= 千米/小时；
（2）当0．9≤t≤3．15时，求d2与t的函数关系式；
（3）已知学生队伍与通讯员的距离不超过3千米时，能用无线对讲机保持联系，试求在上述过程中通讯员离开队伍后他们能用无线对讲机保持联系时t的取值范围．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年福建省南平市建阳市中考适应性数学试卷（解析版） 题型：选择题
某园林队计划由6名工人对200平方米的区域进行绿化，由于施工时增加了2名工人，结果比计划提前3小时完成任务，若每人每小时绿化面积相同，求每人每小时的绿化面积．设每人每小时的绿化面积为x平方米，列出满足题意的方程是（ ）
A．
B．
C．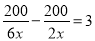
D．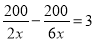
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，其中x满足x2-x-1=0．