Question

【题目】有一块直角三角形纸片，两直角边AC=3cm，BC=4cm，现将直角边AC沿直线AD折叠，使它恰好落在斜边AB上，且与AE重合，求CD的长．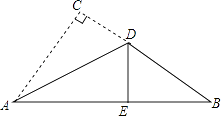

Answer 1

【答案】解：∵有一块直角三角形纸片两直角边AC=3cm，BC=4cm， ∴AB=5cm，
∵将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，
∴DE=CD，AC=AE=3cm，∠DEB=90°，
设CD=xcm，则BD=（4﹣x）cm，
故DE2+BE2=BD2 ，
即x2+（5﹣3）2=（4﹣x）2 ，
解得：x= ，
则CD的长为 cm
【解析】利用翻折变换的性质得出DE=CD，AC=AE=3cm，∠DEB=90°，进而利用勾股定理得出x的值．
【考点精析】本题主要考查了翻折变换（折叠问题）的相关知识点，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．