

|
|


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
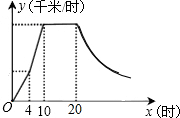 某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(小时/千米),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:
某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(小时/千米),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 一质点P从距原点1个单位的A点处向原点方向跳动,第一次跳动到OA的中点A1处,第二次从A1点跳动到OA1的中点A2处,第三次从A2点跳动到OA2的中点A3处,如此不断跳动下去,则第5次跳动后,该质点到原点O的距离为
一质点P从距原点1个单位的A点处向原点方向跳动,第一次跳动到OA的中点A1处,第二次从A1点跳动到OA1的中点A2处,第三次从A2点跳动到OA2的中点A3处,如此不断跳动下去,则第5次跳动后,该质点到原点O的距离为查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2cm,3cm,4cm |
| B、3cm,5cm,6cm |
| C、2cm,6cm,40cm |
| D、6cm,8cm,10cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com