
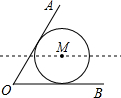 如图,已知∠AOB=60°,半径为2
如图,已知∠AOB=60°,半径为2 的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为
的⊙M与边OA、OB相切,若将⊙M水平向左平移,当⊙M与边OA相交时,设交点为E和F,且EF=6,则平移的距离为 ,再根据垂径定理得EH=
,再根据垂径定理得EH= EF=3,在Rt△EHM′中利用勾股定理计算出HM′=
EF=3,在Rt△EHM′中利用勾股定理计算出HM′= ,则CQ=M′H=
,则CQ=M′H= ,所以MQ=2
,所以MQ=2 -
- =
= ,然后利用含30°的直角三角形三边的关系可得到MM′;
,然后利用含30°的直角三角形三边的关系可得到MM′; ,M′H=
,M′H= ,利用平行线的性质得∠MDC=∠M″DH=∠AOB=60°,则∠HM″D=30°,∠CMD=30°,根据含30°的直角三角形三边的关系可得到M″D和MD,则可得到MM″=6.
,利用平行线的性质得∠MDC=∠M″DH=∠AOB=60°,则∠HM″D=30°,∠CMD=30°,根据含30°的直角三角形三边的关系可得到M″D和MD,则可得到MM″=6.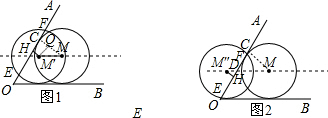
 ,
, EF=
EF= ×6=3,
×6=3, ,
,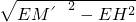 =
= ,
, ,
, -
- =
= ,
,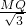 =1,
=1, ,M′H=
,M′H= ,
, ,则DH=
,则DH=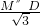 =1,
=1, ,则DC=
,则DC=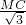 =2,
=2,

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
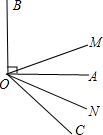
| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:
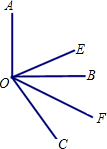 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).
如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com