

分析 (1)由顶点坐标公式直接求出b、c的值;
(2)由于△ABC的三边长易求,面积可知,于联想到希帕霍斯公式S=$\frac{abc}{4R}$,从而直接求出外接圆半径,进而求出圆心M的坐标;
(3)分两种情况:①则△ACB∽△PQB;②△ACB∽△QPB.对于第一种情况,过P作AC的平行线即可得Q点,对于第二种情况,A、C、P、Q四点共圆,由相交弦定理求出BQ的长度,然后求出Q点坐标.
(4)抛物线的上下平移只改变截距,故设出平移后的抛物线解析式的截距,然后可表示出A',B',C'的坐标,设外接圆与y轴的负半轴交于点E,由相交弦定理求出OE长度为定值,即E点就是所求定点.
解答 解:(1)∵抛物线y=-x2+bx+c的顶点D的坐标为(1,4),
∴$\left\{\begin{array}{l}{\frac{-b}{-2}=1}\\{\frac{-4c-{b}^{2}}{-4}=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
抛物线的解析式为y=-x2+2x+3=-(x+1)(x-3),
∴A(-1,0),B(3,0),C(0,3);
(2)连接BC和MB,作MH⊥AB于H,如图1,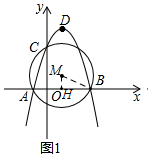
则AB=3-(-1)=4,OC=3,AC=$\sqrt{10}$,BC=3$\sqrt{2}$,
∴${S}_{△ABC}=\frac{1}{2}AB•OC=6$,
设AB=c,BC=a,AC=b,⊙M的半径为R,则由希帕霍斯定理可知:
${S}_{△ABC}=\frac{abc}{4R}$,
∴R=$\frac{abc}{4{S}_{△ABC}}$=$\sqrt{5}$,
∴MB=R=$\sqrt{5}$,
∵MH⊥AB,
∴BH=AH=$\frac{1}{2}AB$=2,
∴MH=$\sqrt{M{B}^{2}-B{H}^{2}}$=1,
∴M(1,1);
(3)①过点P作PQ1∥AC交CB的延长线于点Q1,如图2,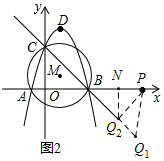
则△ACB∽△PQ1B,
由A、C两点坐标可求得直线AC的解析式为y=3x+3,
设直线PQ1的解析式为y=3x+m,
将P点坐标(7,0)代入可求得m=-21,
∴PQ1的解析式为y=3x-21,
由$\left\{\begin{array}{l}{y=3x-21}\\{y=-x+3}\end{array}\right.$解得$\left\{\begin{array}{l}{x=6}\\{y=-3}\end{array}\right.$,
∴Q1(6,-3);
②作∠BPQ2=∠ACB交CB的延长线于点Q2,则:
△ACB∽△Q2PB,且A、C、P、Q2四点共圆,
由相交弦定理可知:AB•BP=CB•BQ2,
∵AB=4,BC=3$\sqrt{2}$,BP=4,
∴BQ2=$\frac{8\sqrt{2}}{3}$,
作Q2N⊥BP于N,
∵OC=OB,
∴BN=NQ2=$\frac{8}{3}$,
∴ON=OB+BN=$\frac{17}{3}$,
∴Q2($\frac{17}{3}$,-$\frac{8}{3}$),
综上所述,满足要求的Q点坐标为Q1(6,-3),Q2($\frac{17}{3}$,-$\frac{8}{3}$);
(4)设平移后的抛物线解析式为y=-x2+2x+n,(n>3),则C'(0,n),
令-x2+2x+n=0,则x=$1±\sqrt{1+n}$,
∴A'(1-$\sqrt{1+n}$),B'(1+$\sqrt{1+n}$),
设△A′B′C′的外接圆⊙M′与y轴的负半轴的交点为E(0,h),
由相交弦定理可知:OC'•OE=OA'•OB',
∴OE=$\frac{OA'•OB'}{OC'}$=$\frac{(\sqrt{1+n}-1)(\sqrt{1+n}+1)}{n}$=1,
∴E(0,-1),
∴△A′B′C′的外接圆⊙M′始终经过一个定点E(0,-1).
点评 本题是二次函数综合题,主要考查了待定系数法求二次函数与一次函数的解析式、等面积法、希帕霍斯公式、垂径定理、勾股定理、相似三角形的判定与性质、相交弦定理、解二元一次方程组、解一元二次方程等众多知识点,综合性强,难度较大,是一道经典中考压轴题.对于(2)问,利用希帕霍斯定理求出外接圆半径是关键,对于(3)问,分类讨论及相交弦定理的应用是解答要点,对于(4)问,利用相交弦定理计算出外接圆与y轴负半轴的交点是难点所在.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:选择题
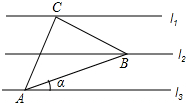 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰△ABC的三个顶点分别在这三条平行直线上,若∠ACB=90°,则sinα的值是( )| A. | $\frac{1}{3}$ | B. | $\frac{6}{17}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点B,D在∠A的一条边上,点C,E在∠A的另一条边上,且DE∥BC,请你写出图中能够成立的一组比例式$\frac{AD}{BD}=\frac{AE}{CE}$(答案不唯一).
如图,点B,D在∠A的一条边上,点C,E在∠A的另一条边上,且DE∥BC,请你写出图中能够成立的一组比例式$\frac{AD}{BD}=\frac{AE}{CE}$(答案不唯一).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,张亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )
如图,张亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )| A. | 经过一点有无数条直线 | B. | 经过两点,有且仅有一条直线 | ||
| C. | 两点间距离的定义 | D. | 两点之间,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
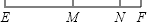 如图,M是线段EF的中点,N是线段MF上一点,如果EF=2a,NF=b,那么下面结论中错误的是( )
如图,M是线段EF的中点,N是线段MF上一点,如果EF=2a,NF=b,那么下面结论中错误的是( )| A. | MN=a-b | B. | MN=$\frac{1}{2}$a | C. | EM=a | D. | EN=2a-b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com