
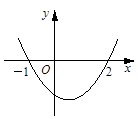
| A.abc>0 | B.a-b+c=0 |
| C.a+b+c>0 | D.4a-2b+c>0 |
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源:不详 题型:解答题
| 时间t(天) | 1 | 3 | 6 | 10 | 36 | … |
| 日销售量m(件) | 94 | 90 | 84 | 76 | 24 | … |
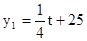 (
( 且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式
且t为整数),后20天每天的价格y2(元/件)与时间t(天)的函数关系式 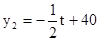 (
( 且t为整数). 下面我们就来研究销售这种商品的有关问题:(1)分析上表中的数据,确定一个满足这些数据的m(件)与t(天)之间的关系式;
且t为整数). 下面我们就来研究销售这种商品的有关问题:(1)分析上表中的数据,确定一个满足这些数据的m(件)与t(天)之间的关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
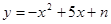 经过点A(1,0),与y轴交于点B。
经过点A(1,0),与y轴交于点B。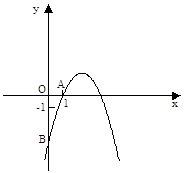
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与
与 轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与
轴交于A、B两点,点C是AB的中点,CD⊥AB且CD=AB.直线BE与 轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
轴平行,点F是射线BE上的一个动点,连接AD、AF、DF.
 ,
, ),AF=
),AF= .
. ,
, ,且AB的长为
,且AB的长为 ,其中
,其中 .如图2,当∠DAF=45时,求
.如图2,当∠DAF=45时,求 的值和∠DFA的正切值.
的值和∠DFA的正切值.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 AB时,求点E的坐标;
AB时,求点E的坐标;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com