

 AB时,求点E的坐标;
AB时,求点E的坐标;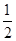 ) (3)
) (3)
 =
= =1
=1 AB
AB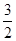
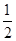
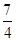
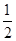 ,-
,- 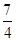 )
)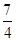 )
)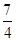 -( -3)=
-( -3)= 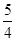
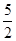
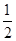 )
)




科目:初中数学 来源:不详 题型:解答题
 在
在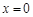 和
和 时的函数值相等。
时的函数值相等。
 的图象与二次函数的图象都经过点
的图象与二次函数的图象都经过点 ,求
,求 和
和 的值;
的值; 轴交于点
轴交于点 (点
(点 在点
在点 的左侧),将二次函数的图象在点
的左侧),将二次函数的图象在点 间的部分(含点
间的部分(含点 和点
和点 )向左平移
)向左平移 个单位后得到的图象记为
个单位后得到的图象记为 ,同时将(2)中得到的直线
,同时将(2)中得到的直线 向上平移
向上平移 个单位。请结合图象回答:当平移后的直线与图象
个单位。请结合图象回答:当平移后的直线与图象 有公共点时,
有公共点时, 的取值范围。
的取值范围。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 在平面直角坐标系中的位置如图所示,
在平面直角坐标系中的位置如图所示, ,
, .抛物线
.抛物线 (
( )经过点
)经过点 和点
和点 ,与
,与 轴分别交于点
轴分别交于点 、
、 (点
(点 在点
在点 左侧),且
左侧),且 ,则下列结论:①
,则下列结论:① ;②
;② ;③
;③ ;④
;④ ;⑤连接
;⑤连接 、
、 ,则
,则 ,其中正确结论的个数为
,其中正确结论的个数为
A. 个 个 | B. 个 个 | C. 个 个 | D. 个 个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=-x2-2; | B.y=-(x-2)2; |
| C.y=-(x+2)2; | D.y=-x2+2. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
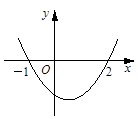
| A.abc>0 | B.a-b+c=0 |
| C.a+b+c>0 | D.4a-2b+c>0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
交y轴于点A,交x轴于点B,C(点B在点C的右侧)。如图,过点A作垂直于y轴的直线l. 在y轴右侧、位于直线l下方的抛物线上任取一点P,过点P作直线PQ平行于y轴交直线l于点Q,交x轴于R,连接AP.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象中,刘敏同学观察得出了下面四条信息:
的图象中,刘敏同学观察得出了下面四条信息:
 ;(2)
;(2)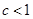 ;(3)
;(3) ;(4)
;(4)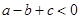 ,你认为其中错误的有( )
,你认为其中错误的有( )| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com