
����Ŀ��(2016�����)��˾��330̨������Ҫһ�������͵�ij�����ƻ����üס������ֻ�����8������֪ÿ�����ֻ���һ��������ͻ���45̨�������Ϊ400Ԫ��ÿ�����ֻ���һ��������ͻ���30̨�������Ϊ280Ԫ��
(1)�����ü��ֻ���x��(xΪ�Ǹ�����)������д����
��һ��
���ü��ֻ��������� / �� | 3 | 7 | x |
���õļ��ֻ���������ͻ��������� / ̨ | 135 | ||
���õ����ֻ���������ͻ��������� / ̨ | 150 |
������
���ü��ֻ��������� / �� | 3 | 7 | x |
���ü��ֻ����ķ���/ Ԫ | 2800 | ||
�������ֻ����ķ��� / Ԫ | 280 |
(2)�����ü��ֻ���x��ʱ�������ֻ������ܷ���ΪyԪ����ȷ������ɴ���������������ʡ���õ��������
���𰸡���1������������2�����ֻ���6�������ֻ���2��
�������������������1���������⣬�ֱ����ÿ�������ÿ�ֻ�����������ͻ����������ͷ��ò������
��2���������������ü��ֻ�������x������ܷ���y��һ�κ�����ϵ����x��һԪһ�β���ʽ��������һ�κ�������������x��ȡֵ��Χ���y����Сֵ��
�⣺��1�����±���


��2��y��400x��(��280x��2 240)��120x��2 240.
�֡�45x��(��30x��240)��330�����x��6.
��120��0��
���ں���y��120x��2 240����y��x�������������
�൱x��6ʱ��yȡ����Сֵ��y��С��2 960.
����ɴ���������������ʡ���õ�����������ü��ֻ���6�������ֻ���2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������ȫƽ��ʽ������ƽ�漸��ͼ�ε��������ʾ��ʵ���ϻ���һЩ�������ʽҲ������������ʽ��ʾ���磺��2a+b����a+b��=2a2+3ab+b2���Ϳ�����ͼ��1����ͼ��2����ͼ�ε������ʾ��

��1����д��ͼ��3������ʾ�Ĵ������ʽ���� ����
��2���Ի�һ������ͼ�Σ�ʹ���������ʾ����a+b����a+2b��=a2+3ab+2b2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABCD��,AB=5,BC=4,�������۵�,ʹ�õ�B�����߶�CD�ĵ�F��,���߶�BE�ij�Ϊ_____________.
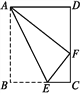
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ߣ�y=ax2+2ax+a2+2��һ������ͼ��ʾ����ô����������y���Ҳ���x�ύ��������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�й涨��ÿ����ˮ18���������ڣ���18�����ף�����ˮ18�������������ֲ�ͬ���շѱ������е��û�ÿ��Ӧ��ˮ��y��Ԫ������ˮ��x�������ף��ĺ�������ͼ����ͼ��ʾ��
��1����ij����ˮ��Ϊ18�����ף���Ӧ��ˮ�Ѷ���Ԫ��
��2����x��18ʱ��y����x�ĺ�������ʽ����С����ij�½�ˮ��81Ԫ�����������ˮ��Ϊ���������ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ��Ŵ���ѧ�����������������м�����һ����Ȥ����ѧ���⣺�������죨�죺ҰѼ�����Ϻ������������������𱱺����������Ϻ�������������ʺ�����ꣿ����˼�ǣ�ҰѼ���Ϻ���ɣ�7��ɵ�����������ӱ�����ɣ�9��ɵ��Ϻ���ҰѼ�������Ϻ��ͱ���ͬʱ��ɣ�����������������ҰѼ�������Ϻ��ͱ���ͬʱ��ɣ�����x���������������⣬�������з�����ȷ���ǣ�������
A. ��9-7��x=1 B. ��9-7��x=1 C. ��![]() +
+![]() ��x=1 D. ��
��x=1 D. ��![]() -
-![]() ��x=1
��x=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B����ͬʱ�������׳�����ǰ��B�أ�����B����������һ�ٶȰ�ԭ·���ٷ��ص�A�أ��ҳ�����ǰ��A�أ���ס���������A�ص�·��Ϊy��ǧ�ף����׳���ʻ��ʱ��Ϊx��ʱ����y��x֮��ĺ���ͼ����ͼ��ʾ
��1����׳���A�ص���B�ص���ʻʱ�䣻
��2����׳�����ʱy��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3�����ҳ�����A��ʱ�׳���A�ص�·�̣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾����A��B���ֻ�������������ij�ֻ����������ֻ����˳�����������������5Сʱ��A�ֻ�������ij��0ʱ��ʼ����������1Сʱ��B�ֻ�����Ҳ��ʼ��������ͼ���߶�OG��ʾA�ֻ����˵İ�����yA(ǧ��)��ʱ��x(ʱ)�ĺ���ͼ��������ͼ���ṩ����Ϣ���������������

(1)��yB����x�ĺ�������ʽ��
(2)���A��B���ֻ�������������5Сʱ����ôB�ֻ����˱�A�ֻ����˶�����˶���ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ����1��3��������4��1������2��1�����Ƚ���ABC��һȷ������ƽ�Ƶõ���A1B1C1 �� ��B�Ķ�Ӧ��B1�������ǣ�1��2�����ٽ���A1B1C1��ԭ��O˳ʱ����ת90��õ���A2B2C2 �� ��A1�Ķ�Ӧ��Ϊ��A2 �� 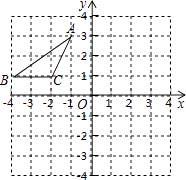
��1��������A1B1C1��
��2��������A2B2C2��
��3������������α任�����У���A������A1����A2��·���ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com