练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在我国古代数学著作《九章算术》中记载了一道有趣的数学问题：“今有凫（凫：野鸭）起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”意思是：野鸭从南海起飞，7天飞到北海；大雁从北海起飞，9天飞到南海．野鸭与大雁从南海和北海同时起飞，经过几天相遇．设野鸭与大雁从南海和北海同时起飞，经过x天相遇，根据题意，下面所列方程正确的是（　　）

    A. （9-7）x=1 B. （9-7）x=1 C. （+）x=1 D. （-）x=1

    【答案】C

    【解析】把两地距离看为1，野鸭每天飞，大雁每天飞，根据相遇问题的路程关系可列出方程.

    把两地距离看为1，野鸭每天飞，大雁每天飞，

    设经过x天相遇，根据题意，得

    （+）x=1

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知A（1，0）、B（0，-1）、C（-1，2）、D（2，-1）、E（4，2）五个点，抛物线y=a（x-1）2+k（a＞0）经过其中的三个点．
    （1）求证：C、E两点不可能同时在抛物线y=a（x-1）2+k（a＞0）上；
    （2）点A在抛物线y=a（x-1）2+k（a＞0）上吗？为什么？
    （3）求a和k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF．

    （1）求证：△BCE≌△DCF；

    （2）当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知线段AB和CD的公共部分BD=AB= CD，线段AB、CD的中点E，F之间距离是10cm，求AB，CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2016·天津)公司有330台机器需要一次性运送到某地，计划租用甲、乙两种货车共8辆，已知每辆甲种货车一次最多运送机器45台，租车费用为400元，每辆乙种货车一次最多运送机器30台，租车费用为280元．

    (1)设租用甲种货车x辆(x为非负整数)，试填写表格：

    表一：

    租用甲种货车的数量 / 辆

    3

    7

    x

    租用的甲种货车最多运送机器的数量 / 台

    135

    租用的乙种货车最多运送机器的数量 / 台

    150

    表二：

    租用甲种货车的数量 / 辆

    3

    7

    x

    租用甲种货车的费用/ 元

    2800

    租用乙种货车的费用 / 元

    280

    (2)若租用甲种货车x辆时，设两种货车的总费用为y元，试确定能完成此项运送任务的最节省费用的租车方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知一次函数y＝kx＋b的图象经过A(－2,－1)，B(1，3)两点，并且交x轴于点C，交y轴于点D.

    （1）求该一次函数的解析式；

    （2）求点C和点D的坐标；

    （3）求△AOB的面积。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    点A、B在数轴上分别表示两个数a、b，A、B两点间的距离记为|AB|，O表示原点．当A、B两点中有一点在原点时，不妨设点A为原点，如图1，则|AB|=|OB|=|b|=|a-b|；当A、B两点都不在原点时，

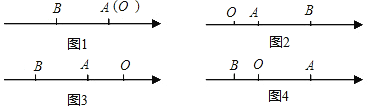
    ①如图2，若点A、B都在原点的右边时，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；

    ②如图3，若点A、B都在原点的左边时，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；

    ③如图4，若点A、B在原点的两边时，|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|．

    回答下列问题：

    （1）综上所述，数轴上A、B两点间的距离为|AB|=______．

    （2）若数轴上的点A表示的数为3，点B表示的数为-4，则A、B两点间的距离为______；

    （3）若数轴上的点A表示的数为x，点B表示的数为-2，则|AB|=______，若|AB|=3，则x的值为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，AC=BC，P是△ABC内一点，且PA=3，PB=1，PC= CD=2，CD⊥CP,求∠BPC的度数

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y=（x+2）2+m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y=kx+b的图象经过该二次函数图象上的点A（﹣1，0）及点B．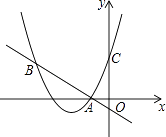

    （1）求二次函数与一次函数的解析式；
    （2）根据图象，写出满足（x+2）2+m≥kx+b的x的取值范围．

    查看答案和解析>>

    同步练习册答案