
【题目】如图,已知线段AB和CD的公共部分BD=![]() AB=
AB= ![]() CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
![]()
【答案】AB=12cm,CD=16cm.
【解析】试题分析:先设BD=xcm,由题意得AB=3xcm,CD=4xcm,AC=6xcm,再根据中点的定义,用含x的式子表示出AE=1.5xcm和CF=2xcm,再根据EF=AC-AE-CF=2.5xcm,且E、F之间距离是EF=10cm,所以2.5x=10,解方程求得x的值,即可求AB,CD的长.
试题解析:解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.
∵点E、点F分别为AB、CD的中点,
∴AE=![]() AB=1.5xcm,CF=
AB=1.5xcm,CF=![]() CD=2xcm.
CD=2xcm.
∴EF=AC-AE-CF=2.5xcm.
∵EF=10cm,
∴2.5x=10,解得:x=4.
∴AB=12cm,CD=16cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.

(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两块含45°角的直角三角板按图1所示的方式放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.
(1)如图1,求证:BE=AD,AF⊥BE;
(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别交BE、BC于点F、G,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在植树节活动中,A班有30人,B班有16人,现要从A班调一部分人去支援B班,使B班人数为A班人数的2倍,那么应从A班调出多少人?如设从A班调x人去B班,根据题意可列方程:__________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
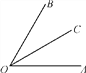
【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB=60°时,求∠AOC的度数;
(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;
(3)当∠AOB=α时,∠EOC=90°,直接写出∠AOE的度数.(用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形ABC中,AB=AC,BC=5 cm,作AB的垂直平分线交AC于点D,连接BD,如果△BCD的周长是17 cm,那么AB的长为( )
A. 12 cm B. 6 cm C. 7 cm D. 5 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com