
【题目】把两块含45°角的直角三角板按图1所示的方式放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.
(1)如图1,求证:BE=AD,AF⊥BE;
(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别交BE、BC于点F、G,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由. 
【答案】
(1)证明:在△BCE和△ACD中,
 ,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠CAD,
在Rt△ACD中,
∵∠CDA+∠CAD=90°,∠BDF=∠CDA
∴∠BDF+∠DBF=90°,
即:AF⊥BE
(2)成立,理由如下:
在△BCE和△ACD中,
∵∠BCE=∠ACD=90°,
∴∠DCE+∠DCB=∠ACB+∠BCD,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
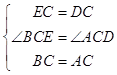 ,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠EBC=∠CAD,
在Rt△ACG中,
∵∠CGA+∠CAG=90°,∠BGF=∠CGA.
∴∠BGF+∠GBF=90°,
即:AF⊥BE
【解析】(1)由SAS判定△ECB≌△DCA,根据全等三角形的性质可知:对应边相等AD=BE、对应角相等∠BEC=∠ADC;加上已知条件来求∠AFE=90°即可;(2)成立,利用已知条件可证明△BCE≌△ACD(SAS),由全等三角形的性质以及已知条件证明即可证明BE=AD,AF⊥BE.
【考点精析】利用旋转的性质对题目进行判断即可得到答案,需要熟知①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。
与x轴交点A(1,0),B(-3,0) .与y轴交点B(0,3),如图1所示,D为抛物线的顶点。
(1)求抛物线的解析式;
(2)如图1若R为y轴上的一个动点,连接AR,则![]()
![]() RB+AR的最小值为
RB+AR的最小值为
(3)在x轴上取一动点P(m,0),![]() ,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.
,过点P作x轴的垂线,分别交抛物线、CD、CB于点Q、F、E,如图2所示,求证EF=EP.
(4)设此抛物线的对称轴为直线MN,在直线MN上取一点T,使∠BTN=∠CTN.直接写出点T的坐标。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD=AE,AD与BE相交于点F. 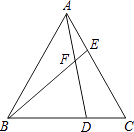
(1)求证:AD=BE;
(2)求∠BFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题。
(1)先化简,再求值:(a+2)2﹣(a+1)(a﹣1),其中a=﹣ ![]() .
.
(2)已知m﹣n=﹣4,mn=2,求下列代数式的值.
①m2+n2
②(m+1)(n﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的个数有( )
①当x=2时,分式 ![]() 的值为零;②每一个命题都有逆命题;③如果a>b,那么ac>bc;④顺次连接任意四边形各边中点得到的四边形是平行四边形;⑤一组对边平行,另一组对边相等的四边形是平行四边形.
的值为零;②每一个命题都有逆命题;③如果a>b,那么ac>bc;④顺次连接任意四边形各边中点得到的四边形是平行四边形;⑤一组对边平行,另一组对边相等的四边形是平行四边形.
A.0
B.1
C.2
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com