
【题目】如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD=AE,AD与BE相交于点F. 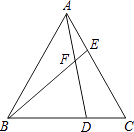
(1)求证:AD=BE;
(2)求∠BFD的度数.
【答案】
(1)证明:∵△ABC为等边三角形,
∴∠BAC=∠C=60°,AB=CA.
在△ABE与△CAD中,
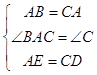 ,
,
∴△ABE≌△CAD(SAS).
∴AD=BE
(2)解:∵△ABE≌△CAD,
∴∠ABE=∠CAD.
∵∠BFD=∠ABE+∠BAD,
∴∠BFD=∠CAD+∠BAD=∠BAC=60°
【解析】(1)根据等边三角形的性质可知∠BAC=∠C=60°,AB=CA,结合AE=CD,可证明△ABE≌△CAD,从而证得结论;(2)根据∠BFD=∠ABE+∠BAD,∠ABE=∠CAD,可知∠BFD=∠CAD+∠BAD=∠BAC=60°.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中 ,AB=8 , BC=6, 点P在边AB上。若将△DAP沿DP折叠 ,使点A落在矩形对角线上的点A,处,则AP的长为__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市6月上旬前5天的最高气温如下(单位:℃):28,29,31,29,32,对于这组数据,众数是_____,中位数是_____,极差是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两块含45°角的直角三角板按图1所示的方式放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.
(1)如图1,求证:BE=AD,AF⊥BE;
(2)将△ABC绕点C顺时针旋转(如图2),连结BE、AD,AD分别交BE、BC于点F、G,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知⊙O的半径是4,△ABC内接于⊙O,AC=![]() .
.
①求∠ABC的度数;
②已知AP是⊙O的切线,且AP=4,连接PC.判断直线PC与⊙O的位置关系,并说明理由;
(2)如图2,已知ABCD的顶点A、B、D在⊙O上,顶点C在⊙O内,延长BC交⊙O于点E,连接DE.求证:DE=DC.

查看答案和解析>>
科目:初中数学 来源: 题型:
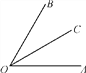
【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB=60°时,求∠AOC的度数;
(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;
(3)当∠AOB=α时,∠EOC=90°,直接写出∠AOE的度数.(用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刘和小李参加射击训练,各射击10次的平均成绩相同,如果他们射击成绩的方差分别是S小刘2=0.6,S小李2=1.4,那么两人中射击成绩比较稳定的是______;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com