
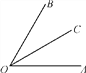
【题目】已知:如图,OC是∠AOB的平分线.
(1)当∠AOB=60°时,求∠AOC的度数;
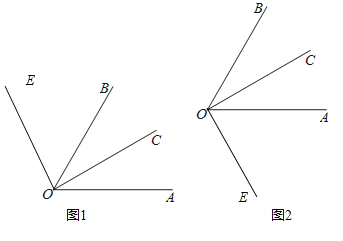
(2)在(1)的条件下,∠EOC=90°,请在图中补全图形,并求∠AOE的度数;
(3)当∠AOB=α时,∠EOC=90°,直接写出∠AOE的度数.(用含α的代数式表示)
【答案】 (1) 30°;(2) 120°或60°;(3)90°+![]() 或90°-
或90°-![]() .
.
【解析】试题分析:(1)直接由角平分线的意义得出答案即可;
(2)分两种情况:OE在OC的上面,OE在OC的下面,利用角的和与差求得答案即可;
(3)类比(2)中的答案得出结论即可.
试题解析:解:(1)∵OC是∠AOB的平分线(已知),∴∠AOC=![]() ∠AOB,∵∠AOB=60°,∴∠AOC=30°.
∠AOB,∵∠AOB=60°,∴∠AOC=30°.
(2)∵OE⊥OC,∴∠EOC=90°,如图1,∠AOE=∠COE+∠COA=90°+30°=120°.
如图2,∠AOE=∠COE﹣∠COA=90°﹣30°=60°.
(3)∠AOE=90°+![]() α或∠AOE=90°﹣
α或∠AOE=90°﹣![]() α.
α.


科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,D、E分别为BC、AC边上的两动点(与点A、B、C不重合),且总使CD=AE,AD与BE相交于点F. 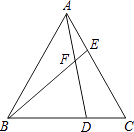
(1)求证:AD=BE;
(2)求∠BFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题。
(1)先化简,再求值:(a+2)2﹣(a+1)(a﹣1),其中a=﹣ ![]() .
.
(2)已知m﹣n=﹣4,mn=2,求下列代数式的值.
①m2+n2
②(m+1)(n﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,D为线段AC的中点,E为线段CB的中点.
(1)如果AB=6 cm,BC=4 cm,试求线段DE的长;
(2)如果AB=a cm,试求线段DE的长;
(3)若C在线段AB的延长线上,且满足AC-BC=b cm,D,E分别为AC,BC的中点,你能猜想出线段DE的长度吗?写出你的结论,不用说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com