
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
【答案】(1)每吨水的政府补贴优惠价2元,市场调节价为3.5元;(2)![]() ;(3)69.
;(3)69.
【解析】
试题分析:(1)设每吨水的政府补贴优惠价为m元,市场调节价为n元,根据题意列出方程组,求解此方程组即可;
(2)根据用水量分别求出在两个不同的范围内y与x之间的函数关系,注意自变量的取值范围;
(3)根据小英家5月份用水26吨,判断其在哪个范围内,代入相应的函数关系式求值即可.
试题解析:(1)设每吨水的政府补贴优惠价为m元,市场调节价为n元.![]() ,解得:
,解得:![]() .
.
答:每吨水的政府补贴优惠价2元,市场调节价为3.5元.
(2)当0≤x≤14时,y=2x;
当x>14时,y=14×2+(x﹣14)×3.5=3.5x﹣21,故所求函数关系式为:![]() ;
;
(3)∵26>14,∴小英家5月份水费为3.5×26﹣21=69元.
答:小英家5月份水费69元.


科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。
(1)求证:AD=AG
(2)AD与AG的位置关系如何,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:如图①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,可知:∠BAD=∠C(不需要证明);
特例探究:如图②,∠MAN=90°,射线AE在这个角的内部,点B、C在∠MAN的边AM、AN上,且AB=AC, CF⊥AE于点F,BD⊥AE于点D.证明:△ABD≌△CAF;
归纳证明:如图③,点BC在∠MAN的边AM、AN上,点EF在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求证:△ABE≌△CAF;
拓展应用:如图④,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,则△ACF与△BDE的面积之和为 .(12分)




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形ABDE和ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC,其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
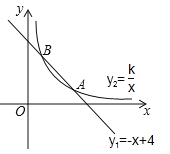
【题目】如图,函数![]() 的图象与函数
的图象与函数![]() (x>0)的图象交于A(m,1),B(1,n)两点.
(x>0)的图象交于A(m,1),B(1,n)两点.
(1)求k,m,n的值;
(2)利用图象写出当x≥1时,![]() 和
和![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二届“红色日记”征文大赛于2020年1月12日正式启动,征文内容分为两部分:“不忘初心”和“红色传承”.其中五位评委给参赛者小亮的征文评分分别为:88、92、90、93、88,则这组数据的众数是 ( )
A.88B.90C.92D.93
查看答案和解析>>
科目:初中数学 来源: 题型:
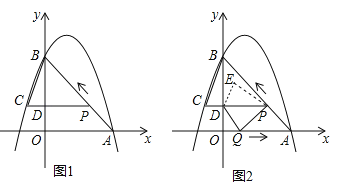
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山西省第22题)综合与实践
问题情境
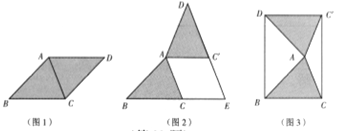
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(![]() )沿对角线AC剪开,得到
)沿对角线AC剪开,得到![]() 和
和![]() .
.
操作发现
(1)将图1中的![]() 以A为旋转中心,逆时针方向旋转角
以A为旋转中心,逆时针方向旋转角![]() ,使
,使 ![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长BC 和
,分别延长BC 和![]() 交于点E,则四边形
交于点E,则四边形![]() 的状是 ;
的状是 ;
(2)创新小组将图1中的![]() 以A为旋转中心,按逆时针方向旋转角
以A为旋转中心,按逆时针方向旋转角![]() ,使
,使![]() ,得到如图3所
,得到如图3所
示的![]() ,连接DB,
,连接DB,![]() ,得到四边形
,得到四边形![]() ,发现它是矩形.请你证明这个论;
,发现它是矩形.请你证明这个论;
(3)缜密小组在创新小组发现结论的基础上,量得图3中BC=13cm,AC=10cm,然后提出一个问题:将![]() 沿着射线DB方向平移acm,得到
沿着射线DB方向平移acm,得到![]() ,连接
,连接![]() ,
,![]() ,使四边形
,使四边形![]() 恰好为正方形,求a的值.请你解答此问题;
恰好为正方形,求a的值.请你解答此问题;
(4)请你参照以上操作,将图1中的![]() 在同一平面内进行一次平移,得到
在同一平面内进行一次平移,得到![]() ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com