
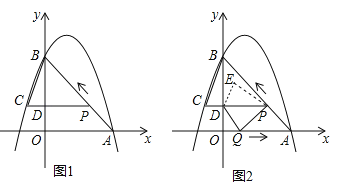
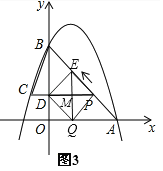
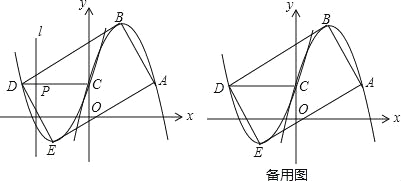
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
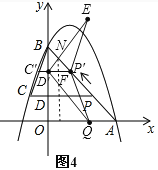
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
【答案】(1)![]() ;(2)4;(3)
;(2)4;(3)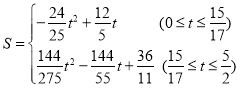 .
.
【解析】
试题分析:(1)直接将A、B两点的坐标代入列方程组解出即可;
(2)如图1,要想求△BCP的面积,必须求对应的底和高,即PC和BD;先求OD,再求BD,PC是利用点P和点C的横坐标求出,要注意符号;
(3)分两种情况讨论:①△DPE完全在△OAB中时,即当![]() 时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当
时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当![]() 时,如图4所示,△PDN就是重合部分的面积S.
时,如图4所示,△PDN就是重合部分的面积S.
试题解析:(1)把A(3,0),B(0,4)代入![]() 中得:
中得:
![]() ,解得:
,解得:![]() ,∴解析式为:
,∴解析式为:![]() ;
;
(2)如图1,当![]() 时,AP=2t,∵PC∥x轴,∴
时,AP=2t,∵PC∥x轴,∴![]() ,∴
,∴![]() ,∴OD=
,∴OD=![]() =
=![]() =
=![]() ,当y=
,当y=![]() 时,
时,![]() =
=![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,∴C(﹣1,
,∴C(﹣1,![]() ),由
),由![]() ,得
,得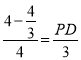 ,则PD=2,∴S△BCP=
,则PD=2,∴S△BCP=![]() ×PC×BD=
×PC×BD=![]() =4;
=4;
(3)分两种情况讨论:①如图3,当点E在AB上时,由(2)得OD=QM=ME=![]() ,∴EQ=
,∴EQ=![]() ,由折叠得:EQ⊥PD,则EQ∥y轴,∴
,由折叠得:EQ⊥PD,则EQ∥y轴,∴![]() ,∴
,∴ ,∴t=
,∴t=![]() ,同理得:PD=
,同理得:PD=![]() ,∴当
,∴当![]() 时,S=S△PDQ=
时,S=S△PDQ=![]() ×PD×MQ=
×PD×MQ=![]() ,
,![]() ;
;
②当![]() 时,如图4,P′D′=
时,如图4,P′D′=![]() ,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,
,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,![]() ),∵AB的解析式为:
),∵AB的解析式为:![]() ,D′E的解析式为:
,D′E的解析式为:![]() ,则交点N(
,则交点N(![]() ,
,![]() ),∴S=S△P′D′N=
),∴S=S△P′D′N=![]() ×P′D′×FN=
×P′D′×FN=![]() ,∴
,∴![]() .
.
综上所述: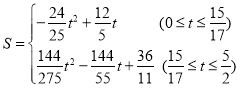 .
.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 任何一个有理数的绝对值都是正数
B. 有理数可以分为正有理数和负有理数
C. 多顶式3πa3+4a2-8的次数是4
D. x的系数和次数都是1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
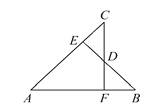
【题目】如图,点E,F分别在∠CAB的边AC,AB上,若AB=AC,AE=AF,BE与CF交于点D,给出结论:①△ABE≌△ACF;②BD=DE;③△BDF≌△CDE;④点D在∠BAC的平分线上.其中正确的结论有____(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
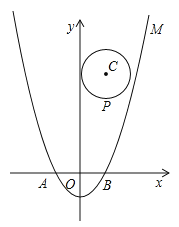
【题目】如图,在平面直角坐标系xOy中,将二次函数![]() 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求![]() 的最大值;
的最大值;
(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
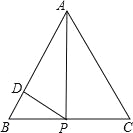
【题目】(2016浙山东省泰安市第20题)如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.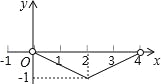
B.
C.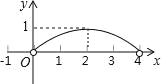
D.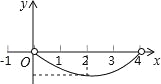
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2,点A,B的对应点分别为点D,E.
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com