
【题目】(2016山西省第22题)综合与实践
问题情境
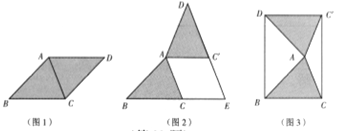
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(![]() )沿对角线AC剪开,得到
)沿对角线AC剪开,得到![]() 和
和![]() .
.
操作发现
(1)将图1中的![]() 以A为旋转中心,逆时针方向旋转角
以A为旋转中心,逆时针方向旋转角![]() ,使
,使 ![]() ,得到如图2所示的
,得到如图2所示的![]() ,分别延长BC 和
,分别延长BC 和![]() 交于点E,则四边形
交于点E,则四边形![]() 的状是 ;
的状是 ;
(2)创新小组将图1中的![]() 以A为旋转中心,按逆时针方向旋转角
以A为旋转中心,按逆时针方向旋转角![]() ,使
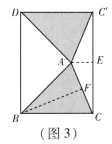
,使![]() ,得到如图3所
,得到如图3所
示的![]() ,连接DB,
,连接DB,![]() ,得到四边形
,得到四边形![]() ,发现它是矩形.请你证明这个论;
,发现它是矩形.请你证明这个论;
(3)缜密小组在创新小组发现结论的基础上,量得图3中BC=13cm,AC=10cm,然后提出一个问题:将![]() 沿着射线DB方向平移acm,得到
沿着射线DB方向平移acm,得到![]() ,连接
,连接![]() ,
,![]() ,使四边形
,使四边形![]() 恰好为正方形,求a的值.请你解答此问题;
恰好为正方形,求a的值.请你解答此问题;
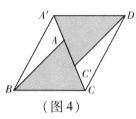
(4)请你参照以上操作,将图1中的![]() 在同一平面内进行一次平移,得到
在同一平面内进行一次平移,得到![]() ,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.
【答案】(1)、菱形;(2)、证明过程见解析;(3)、![]() 或
或![]() ;(4)、平行四边形.
;(4)、平行四边形.
【解析】
试题分析:(1)、利用旋转的性质和菱形的判定证明;(2)、利用旋转的性质以及矩形的判定证;(3)、利用平移行性质和正方形的判定证明,需注意射线这个条件,所以需要分两种情况当点![]() 在边
在边![]() 上和点
上和点![]() 在边
在边![]() 的延长线上时;(4)、开放型题目,答对即可.
的延长线上时;(4)、开放型题目,答对即可.
试题解析:(1)、菱形
(2)、作![]() 于点E. 由旋转得
于点E. 由旋转得![]() ,
,![]() .
.
![]() 四边形ABCD是菱形,
四边形ABCD是菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
同理![]() ,
,![]() ,又
,又![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
又![]() ,
,![]() ,
,![]() , ∴四边形
, ∴四边形![]() 是矩形
是矩形
(3)、过点B作![]() ,垂足为F,
,垂足为F,![]() ,
, ![]() .
.
在Rt![]() 中,
中,![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
, ![]() .
.
![]() ∽
∽![]() ,
,![]() ,即
,即![]() ,解得
,解得![]() ,
,
![]() ,
,![]() ,
,![]() .
.
当四边形![]() 恰好为正方形时,分两种情况:
恰好为正方形时,分两种情况:
①点![]() 在边
在边![]() 上.
上.![]() .
.
②点![]() 在边
在边![]() 的延长线上,
的延长线上,![]()
综上所述,a的值为![]() 或
或![]() .
.
(4)、答案不唯一.
平移及构图方法:将![]() 沿着射线CA方向平移,平移距离为
沿着射线CA方向平移,平移距离为![]() 的长度,得到
的长度,得到![]() ,连接
,连接![]() .
.
结论:四边形是平行四边形


科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由长度为1个单位的若干小正方形组成的网格图中,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)三角形ABC的面积为
(3)以AC为边作与△ABC全等的三角形(只要作出一个符合条件的三角形即可);
(4)在直线l上找一点P,使PB+PC的长最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
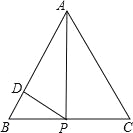
【题目】(2016浙山东省泰安市第20题)如图,正△ABC的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是( )
A.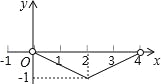
B.
C.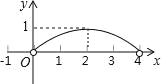
D.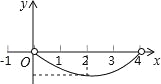
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】命题“如果两个角相等,那么它们都是直角”的逆命题是( )
A.如果两个角不相等,那么它们都不是直角
B.如果两个角都不是直角,那么这两个角不相等
C.如果两个角都是直角,那么这两个角相等
D.相等的两个角都是直角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车的油箱中现有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km,写出表示y与x的函数关系的式子_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知开口向下的抛物线y1=ax2﹣2ax+1过点A(m,1),与y轴交于点C,顶点为B,将抛物线y1绕点C旋转180°后得到抛物线y2,点A,B的对应点分别为点D,E.
(1)直接写出点A,C,D的坐标;
(2)当四边形ABCD是矩形时,求a的值及抛物线y2的解析式;
(3)在(2)的条件下,连接DC,线段DC上的动点P从点D出发,以每秒1个单位长度的速度运动到点C停止,在点P运动的过程中,过点P作直线l⊥x轴,将矩形ABDE沿直线l折叠,设矩形折叠后相互重合部分面积为S平方单位,点P的运动时间为t秒,求S与t的函数关系.
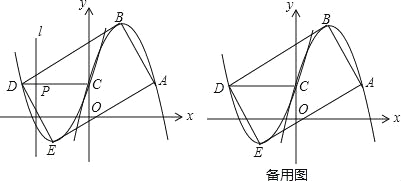
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com