
【题目】在锐角三角形ABC中,AH是BC边上的高,分别以AB,AC为一边,向外作正方形ABDE和ACFG,连接CE,BG和EG,EG与HA的延长线交于点M,下列结论:①BG=CE;②BG⊥CE;③AM是△AEG的中线;④∠EAM=∠ABC,其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
【解析】试题分析:根据正方形的性质可得AB=AE,AC=AG,∠BAE=∠CAG=90°,然后求出∠CAE=∠BAG,再利用“边角边”证明△ABG和△AEC全等,根据全等三角形对应边相等可得BG=CE,判定①正确;设BG、CE相交于点N,根据全等三角形对应角相等可得∠ACE=∠AGB,然后求出∠CNG=90°,根据垂直的定义可得BG⊥CE,判定②正确;过点E作EP⊥HA的延长线于P,过点G作GQ⊥AM于Q,根据同角的余角相等求出∠ABH=∠EAP,再利用“角角边”证明△ABH和△EAP全等,根据全等三角形对应角相等可得∠EAM=∠ABC判定④正确,全等三角形对应边相等可得EP=AH,同理可证GQ=AH,从而得到EP=GQ,再利用“角角边”证明△EPM和△GQM全等,根据全等三角形对应边相等可得EM=GM,从而得到AM是△AEG的中线,故③正确. 综上所述,①②③④结论都正确.
故选:A.



科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,∠AOB=100°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)当△AOD是等腰三角形时,求α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价和市场价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小明家5月份用水26吨,则他家应交水费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别在∠CAB的边AC,AB上,若AB=AC,AE=AF,BE与CF交于点D,给出结论:①△ABE≌△ACF;②BD=DE;③△BDF≌△CDE;④点D在∠BAC的平分线上.其中正确的结论有____(填写序号).
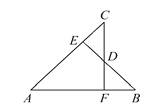
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com