【题目】如图，点O是等边△ABC内一点，∠AOB=100°，∠BOC=α．以OC为一边作等边三角形OCD，连接AC、AD．

（1）当α=150°时，试判断△AOD的形状，并说明理由；

（2）当△AOD是等腰三角形时，求α的度数．

参考答案：

【答案】（1）△OCD是等边三角形，理由见解析；（2）当α为130°、100°、160°时，△AOD是等腰三角形．

【解析】

试题分析：（1）首先根据已知条件可以证明△BOC≌△ADC，然后利用全等三角形的性质可以求出∠ADO的度数，由此即可判定△AOD的形状；

（2）利用（1）和已知条件及等腰三角形的性质即可求解．

解：（1）∵△OCD是等边三角形，

∴OC=CD，

∵△ABC是等边三角形，

∴BC=AC，

∵∠ACB=∠OCD=60°，

∴∠BCO=∠ACD，

在△BOC与△ADC中，

，

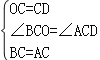∴△BOC≌△ADC，

∴∠BOC=∠ADC，

∵∠BOC=α=150°，∠ODC=60°，

∴∠ADO=150°﹣60°=90°，

∴△ADO是直角三角形；

（2）∵∠COB=∠CAD=α，∠AOD=200°﹣α，∠ADO=α﹣60°，∠OAD=40°，

①要使AO=AD，需∠AOD=∠ADO，

∴200°﹣α=α﹣60°，

∴α=130°；

②要使OA=OD，需∠OAD=∠ADO，

∴α﹣60°=40°，

∴α=100°；

③要使OD=AD，需∠OAD=∠AOD，

∴200°﹣α=40°，

∴α=160°．

所以当α为130°、100°、160°时，△AOD是等腰三角形．

关闭